Esito finale di accelerazione e decelerazione delle maree

Quindi, so che la Luna sperimenta l'accelerazione delle maree dalla Terra. E, da quello che ho letto, se non fosse per il fatto che il sole avrebbe fatto bollire gli oceani e li avrebbe inghiottiti entrambi per primi, tra circa 50 miliardi di anni la Luna sarebbe geosincrona.

Ero curioso di sapere se l'accelerazione delle maree potesse mai far sfuggire un satellite, e la risposta breve sembra essere, sì, è possibile. È preciso? E se sì, quali fattori si aggiungono ad esso?

1. Un pianeta a rotazione più veloce porta anche a maree più avanti e ha più energia da perdere prima di essere completamente bloccato. Molto strettamente correlato, un satellite più lontano orbita più lentamente, con conseguente maree più avanti e richiede meno energia per fuggire. Questo sembra ovvio: più velocemente il pianeta sta ancora ruotando mentre il satellite è più lontano, più è probabile che fugga.
2. Un pianeta più fluido sperimenterebbe maree più forti, che lo rallenterebbero più velocemente, ma accelererebbero sicuramente il satellite più velocemente. Un fluido più viscoso dell'acqua potrebbe sperimentare maree più deboli, ma penso che sarebbero più avanti. Penso che più fluido sia sicuramente più efficace, ma sembra meno ovvio del primo punto.
3. Un pianeta più grande avrebbe la sua orbita rallentata meno dall'accelerazione delle maree, ma avrebbe una spinta più forte per fuggire. Un satellite più grande causerebbe maree più forti e più forza di marea, ma richiederebbe più forza per accelerare e rallenterebbe il pianeta più rapidamente. Non so davvero quale abbia l'effetto più forte ...

Quindi questa è la domanda 1: è davvero possibile per l'accelerazione delle maree lanciare un satellite nello spazio prima che il pianeta sia bloccato in modo ordinato e, in tal caso, la dimensione di entrambi gli oggetti ha un impatto su di esso o solo fluidità e periodi relativi?

Quindi, mi chiedevo quale fosse la decelerazione delle maree e lo schianto sul pianeta. Sembra ovvio che qualsiasi satellite in orbita retrogrado non smetterebbe mai di decelerare, quindi alla fine tutti sarebbero fatti a pezzi e si schianterebbero sul loro pianeta. Per i satelliti non retrogade, un articolo che ho letto implicava che tutti avrebbero lo stesso destino ... Il che implica che la rotazione del pianeta accelererà sempre più lentamente dell'orbita di caduta del satellite. È vero? Altrimenti, sembra che ci debbano essere casi in cui la rotazione del pianeta raggiunge, e finiscono di nuovo bloccati in ordine.

Quindi questa è la domanda 2: tutti i satelliti che non rallentano in ordine decrescente finiranno per schiantarsi sul loro pianeta, o è possibile che il pianeta lo raggiunga, date le giuste condizioni di partenza?

Modifica: non ho davvero trovato ulteriori informazioni su questo. C'è qualcuno che abbia familiarità con le equazioni rilevanti, chi conosce la risposta?

Quindi questa è la domanda 1: è davvero possibile per l'accelerazione delle maree lanciare un satellite nello spazio prima che il pianeta sia bloccato in modo ordinato e, in tal caso, la dimensione di entrambi gli oggetti ha un impatto su di esso o solo fluidità e periodi relativi?

Durante il processo di bloccaggio, il momento angolare di uno viene inserito nell'altro fino a quando i periodi coincidono. La destinazione finale dipende dal momento iniziale di entrambi gli oggetti e dal momento di inerzia. Ad esempio, se rendessi la luna meno massiccia, o la terra più massiccia o con una rotazione più veloce, la configurazione finale del sistema avrebbe un'orbita più grande.

Potresti certamente creare un sistema in cui la configurazione teorica finale ha una distanza dal satellite che va oltre la sfera di Hill della primaria. Un tale sistema dovrebbe eventualmente separarsi.

La fluidità potrebbe cambiare la velocità con cui viene raggiunta la destinazione finale, ma non la sua configurazione.

Tutti i satelliti che rallentano in modo ordinato e non retrogati finiranno per schiantarsi contro il loro pianeta, o è possibile che il pianeta riesca a raggiungerli date le giuste condizioni di partenza?

Ogni oggetto sta trasferendo la stessa quantità di momento angolare. Ma la risposta di ciascun oggetto dipende (almeno inizialmente) dalle dimensioni relative dei loro momenti di inerzia. Per un sistema in cui il satellite è (relativamente) piccolo o in cui la differenza nelle velocità di rotazione è grande, l'impatto è inevitabile. Il primario non può accelerare abbastanza velocemente da tenere il passo con la crescente velocità del partner discendente.

Ma quando la differenza nei periodi è piccola e il primario è abbastanza piccolo / abbastanza lontano, gli oggetti si bloccherebbero prima dell'impatto.

Ti sei perso il fattore più importante, ovvero quanto è vicino il sole e come risultato della distanza dal sole e della massa relativa, la sfera di Hill e la distanza approssimativa in cui termina la distanza orbitale stabile .

Il momento angolare per valutare la distanza con cui la luna viene allontanata dal pianeta è un'interessante combinazione di formule e potrebbe probabilmente essere calcolata in base ai fattori menzionati, densità, massa, dimensioni, forma e massa degli oceani liquidi sulla superficie, velocità di rotazione, ecc. Probabilmente non c'è un'approssimazione così complessa che potrebbe essere elaborata per scenari di differenza per mostrare fino a che punto una luna migrerebbe prima che il sistema si blocchi in modo ordinato e quanto tempo impiegherebbe. (alcuni sistemi meno interattivi potrebbero impiegare trilioni o quadrilioni di anni o più per raggiungere una posizione relativamente definitiva, rispetto ai circa 50 miliardi circa di tempo per il sistema Terra-Luna per bloccarsi in ordine.

Ma se consideriamo il Sole-Terra-Luna come esempio, il più importante sul fatto che la Terra perda la sua luna è quanto si estende la parte stabile della Sfera della Collina, che, se le masse di tutti e 3 gli oggetti sono quello che sono ora, il fattore principale è quanto è vicina la Terra al Sole. Se la Terra fosse vicina al Sole come Venere, probabilmente la Luna sarebbe fuggita, ma ci sarebbe voluto del tempo. Se la Terra fosse vicina al sole come Mercurio (in media), avrebbe perso la Luna molto tempo fa.

OK, penso di avere una semplice strada per le tue altre domande, almeno un buon punto di partenza. Momento angolare.

Se consideriamo un sistema orbitale a due corpi, l'effetto di marea sull'orbita è piuttosto semplice. Considerando i sistemi in cui il rigonfiamento ruota davanti alla luna, la luna viene lentamente allontanata dal pianeta e la rotazione del pianeta diminuisce gradualmente.

In questo sistema a due corpi la luna non sfugge mai perché in un sistema a due corpi, le orbite rimangono stabili su un'enorme distanza, la domanda diventa essenzialmente, quanto si allontana la luna e quanto tempo impiega fino a quando il sistema è bloccato in modo ordinato dove si trova , almeno matematicamente, raggiunge il suo stato finale.

Il 3 ° corpo nella foto (il Sole) ha un effetto in un paio di modi. La relazione tra la massa e la distanza relative del Sole e del Pianeta determina il confine approssimativo della regione stabile della Sfera della Collina, oltre la quale probabilmente la luna fugge. Il Sole inoltre rimorchia la Luna, creando perturbazioni nella sua orbita e rendendola non curcolare, dove, in confronto, il sistema dei due corpi con la luna che viene allontanata si mosse per diventare circolare.

Per i Nani rossi, dove i pianeti sono vicini alla stella, il pianeta che diventa in ordine vicino alla stella nana rossa diventa molto più probabile (anche se qualche blocco parziale come il rapporto orbita 3/2 di Mercurio rispetto alla rotazione può accadere occasionalmente), ma nella maggior parte casi, con una stella nana rossa e pianeti relativamente vicini, il pianeta si blocca in modo ordinato alla stella e ruota efficacemente più lentamente rispetto alla luna, portando a un'orbita in decomposizione per le lune verso i loro pianeti in sistemi nani rossi. Anche la regione orbitale stabile in tali sistemi sarebbe molto più piccola. Il sole è un fattore significativo nel movimento delle lune verso o dai pianeti.

Ma tornando al sistema a 2 corpi e stimando l'effetto delle maree, sapendo che la luna non potrà mai sfuggire a un sistema a due corpi chiuso, la domanda quindi risolverà fino a che punto la Luna può muoversi dal pianeta e quanto tempo impiegherà viene raggiunto il bloccaggio reciproco delle maree.

La distanza che la Luna può percorrere dal pianeta può essere stimata dal momento angolare totale del sistema, quindi hai ragione che la velocità di rotazione iniziale è un fattore, così come la massa relativa tra il Pianeta e la Luna. Una luna più massiccia crea un rigonfiamento di marea più grande sul pianeta, che si traduce nella Luna che si allontana dal pianeta più velocemente di una luna meno massiccia. Allo stesso tempo, la luna più massiccia richiede più momento angolare mentre si allontana dal pianeta, quindi si sposta meno lontano. Una luna meno massiccia si muove ulteriormente ma impiega molto più tempo per arrivarci e anche il blocco delle maree impiega più tempo per accadere.

Un pianeta più fluido sperimenterebbe maree più forti, che lo rallenterebbero più velocemente, ma accelererebbero sicuramente il satellite più velocemente. Un fluido più viscoso dell'acqua potrebbe sperimentare maree più deboli, ma penso che sarebbero più avanti. Penso che più fluido sia sicuramente più efficace, ma sembra meno ovvio del primo punto.

Non è corretto affermare che un pianeta più fluido sperimenterebbe maree più forti. Dire che sperimenterebbe maree più alte rispetto a se fosse solido sarebbe più preciso. Le maree che il pianeta sperimenta dipendono dalla massa e dalla distanza della Luna e dalle dimensioni del pianeta, quindi essendo la Luna uguale, le maree sarebbero le stesse se il pianeta è liquido o solido. I fluidi sono meno rigidi, quindi sono migliori nel fare le maree, ma ci sono anche maree sulla terra. Sulla Terra sono chiamati maree .

La marea più alta spinge efficacemente meglio la Luna e rallenta il pianeta più rapidamente e il liquido risponde alle maree in modo più efficiente, quindi i pianeti con una superficie liquida muovono le loro lune in modo più efficiente e veloce rispetto ai pianeti senza una superficie liquida. Anche la forma degli oceani conta. Il Pacifico più ampio ha maree più grandi rispetto all'Atlantico più stretto.

fonte

Non credo che la viscosità dei liquidi contenga. Flusso di liquidi, solidi no e padre avanti non è neanche corretto. I pianeti generalmente ruotano come un'unità, sebbene vi siano piccole discrepanze tra la velocità di rotazione tra il nucleo e il mantello, l'intero pianeta ruota e il rigonfiamento delle maree ruota con esso. I liquidi sono più efficienti e sporgenti, ma non in entrambi i casi il rigonfiamento si sposta in avanti con la rotazione del pianeta ad angoli uguali davanti alla luna.

Un pianeta più grande avrebbe la sua orbita rallentata meno dall'accelerazione delle maree, ma avrebbe una spinta più forte per fuggire. Un satellite più grande causerebbe maree più forti e più forza di marea, ma richiederebbe più forza per accelerare e rallenterebbe il pianeta più rapidamente. Non so davvero quale abbia l'effetto più forte ...

Qui devi stare attento perché è un po 'più complicato. La forza di marea che un pianeta sperimenta dalla sua luna ha a che fare con la massa della luna, la distanza della luna, ma anche la massa del pianeta e il raggio del pianeta.

Guardando i numeri:

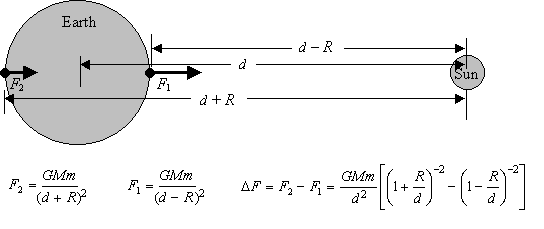
fonte

la seconda parte della formula è piuttosto complicata, $[(1 + R/d)^{-2} - (1 - R/d)^{-2}]$

ma se elaborate la matematica per lune abbastanza distanti, la differenza nella forza delle maree dalla parte lontana del pianeta alla parte vicina riguarda:

Quindi guardando il sistema Terra-Luna, ignorando il sole per ora.

Se rendi la Terra delle stesse dimensioni ma il doppio della massa, la forza della marea raddoppierà ma raddoppierebbe anche la gravità della superficie terrestre, il che darebbe all'acqua dell'oceano il doppio del peso con uguale massa, la forza sulla Luna dovrebbe essere simile, ma una Terra più pesante impiegherebbe più tempo a rallentare, quindi l'effetto sarebbe che la Luna si muoverà ulteriormente, non meno lontano.

Se mantieni la stessa densità e ingrandisci la Terra, dì 8 volte la massa, quindi il doppio del diametro. La forza di marea che la Luna esercita sulla nostra nuova super-terra sarebbe 16 volte maggiore, ma la gravità sulla superficie terrestre solo il doppio. Ciò significa che allargando il pianeta, la Luna si allontana effettivamente più velocemente. Il pianeta più grande (ma di uguale densità) dovrebbe rallentare all'incirca alla stessa velocità ma quando la Luna si allontana tale velocità rallenterebbe.

Parte della matematica delle maree diventa confusa per me. La forza di marea inversa che allontana le lune dai pianeti diminuisce significativamente con la distanza. La forza di marea diminuisce con il cubo della distanza. La forza del rigonfiamento delle maree può scendere ancora più velocemente di quella perché l'angolo diminuisce con la distanza (immagino che diminuisca del 4 ° potere), quindi, man mano che la distanza della Luna dalla Terra raddoppia, la velocità che si allontana diminuisce di (circa), 16 volte. (((Penso))).

Quindi, se rendi la Terra 8 volte più massiccia, e il doppio del raggio, la forza di marea aumenta di 16, ma se la Luna si muove due volte più in là, la forza di marea diminuisce di 16, il che è abbastanza pulito da annullarsi. Il rapporto distanza / gravità, supponendo che la Luna non cambi e la densità del pianeta non cambi, è 1 a 1, che è quello che mi aspetterei.

Probabilmente è più lungo di quanto dovrebbe essere e probabilmente ha bisogno di molta pulizia, ma devo chiamarlo un giorno, quindi lo guarderò domani.