Il problema può essere risolto in O (polilogo (b)).
Definiamo f(d, n)il numero di numeri interi con cifre decimali fino a d con somma delle cifre inferiore o uguale a n. Si può vedere che questa funzione è data dalla formula

Deriviamo questa funzione, iniziando con qualcosa di più semplice.
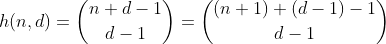
La funzione h conta il numero di modi per scegliere d - 1 elementi da un set multiplo contenente n + 1 elementi diversi. È anche il numero di modi per suddividere n in d bin, che può essere facilmente visto costruendo d - 1 recinti attorno a n uno e riassumendo ogni sezione separata. Esempio per n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Quindi, h conta tutti i numeri con una somma di cifre di cifre n e d. Tranne che funziona solo per n meno di 10, poiché le cifre sono limitate a 0 - 9. Per risolvere questo problema per i valori 10 - 19, è necessario sottrarre il numero di partizioni che hanno un cestino con un numero maggiore di 9, che chiamerò bin overflow da ora in poi.
Questo termine può essere calcolato riutilizzando h nel modo seguente. Contiamo il numero di modi per partizionare n - 10, quindi scegliamo uno dei bin in cui inserire il 10, il che si traduce nel numero di partizioni con un cestino overflow. Il risultato è la seguente funzione preliminare.
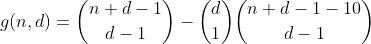
Continuiamo in questo modo per n minore o uguale a 29, contando tutti i modi di partizionare n - 20, quindi scegliendo 2 bin in cui inserire i 10, contando così il numero di partizioni contenenti 2 bin overflow.
Ma a questo punto dobbiamo stare attenti, perché abbiamo già contato le partizioni con 2 bidoni overflow nel termine precedente. Non solo, ma in realtà li abbiamo contati due volte. Facciamo un esempio e diamo un'occhiata alla partizione (10,0,11) con la somma 21. Nel termine precedente, abbiamo sottratto 10, calcolato tutte le partizioni dei restanti 11 e messo il 10 in uno dei 3 bin. Ma questa particolare partizione può essere raggiunta in due modi:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Dal momento che abbiamo contato anche queste partizioni una volta nel primo termine, il conteggio totale delle partizioni con 2 contenitori in overflow è pari a 1 - 2 = -1, quindi dobbiamo contarle ancora una volta aggiungendo il termine successivo.
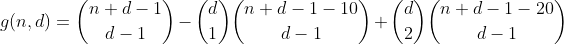
Ripensandoci un po 'di più, scopriamo presto che il numero di volte in cui una partizione con un numero specifico di bin overflow viene contata in un termine specifico può essere espressa dalla seguente tabella (colonna i rappresenta il termine i, riga j partizioni con j overflown bidoni).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Sì, è il triangolo di Pascal. L'unico conteggio a cui siamo interessati è quello nella prima riga / colonna, ovvero il numero di partizioni con zero bin overflow. E poiché la somma alternata di ogni riga ma la prima è uguale a 0 (ad esempio 1 - 4 + 6 - 4 + 1 = 0), è così che ci liberiamo di loro e arriviamo alla penultima formula.
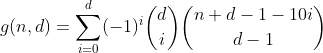
Questa funzione conta tutti i numeri con cifre d con una somma di cifre pari a n.
Ora, che dire dei numeri con cifra-somma inferiore a n? Possiamo usare una ricorrenza standard per i binomi più un argomento induttivo, per dimostrarlo
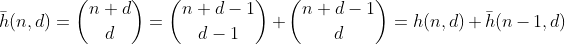
conta il numero di partizioni con somma cifre al massimo n. E da questo f si può derivare usando gli stessi argomenti di g.
Usando questa formula, possiamo ad esempio trovare il numero di numeri pesanti nell'intervallo da 8000 a 8999 poiché 1000 - f(3, 20), poiché ci sono migliaia di numeri in questo intervallo, e dobbiamo sottrarre il numero di numeri con somma delle cifre inferiore o uguale a 28 tenendo conto del fatto che la prima cifra contribuisce già 8 alla somma delle cifre.
Come esempio più complesso, diamo un'occhiata al numero di numeri pesanti nell'intervallo 1234..5678. Possiamo prima andare da 1234 a 1240 a passi di 1. Quindi andiamo da 1240 a 1300 a passi di 10. La formula sopra ci dà il numero di numeri pesanti in ciascuno di tali intervalli:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Ora andiamo dal 1300 al 2000 a passi di 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
Da 2000 a 5000 con incrementi di 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Ora dobbiamo ridurre nuovamente le dimensioni del gradino, passando da 5000 a 5600 a passi di 100, da 5600 a 5670 a passi di 10 e infine da 5670 a 5678 a passi di 1.
Un esempio di implementazione di Python (che nel frattempo ha ricevuto lievi ottimizzazioni e test):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Modifica : ha sostituito il codice con una versione ottimizzata (che sembra persino più brutta del codice originale). Ho anche risolto alcuni casi angolari mentre ero lì. heavy(1234, 100000000)impiega circa un millisecondo sulla mia macchina.
