È possibile evitare il passaggio di "divisione" in un tipo di unione?

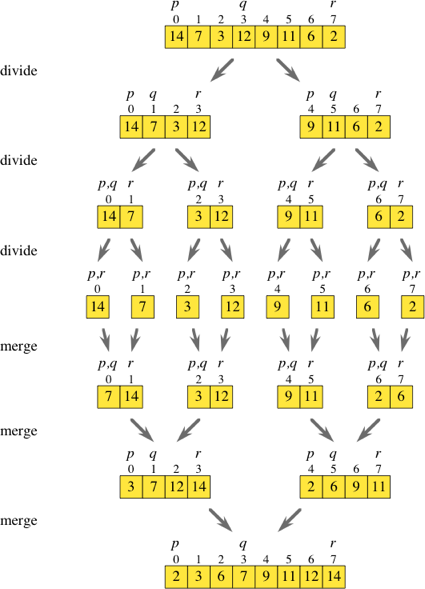
Unisci ordinamento

Quindi unire l'ordinamento è un algoritmo di divisione e conquista. Mentre stavo guardando il diagramma sopra, stavo pensando se fosse possibile bypassare sostanzialmente tutti i passaggi di divisione.

Se si scorreva sull'array originale mentre si saltava di due, è possibile ottenere gli elementi nell'indice i e i + 1 e inserirli nei propri array ordinati. Una volta che hai tutti questi sotto-array ([7,14], [3,12], [9,11] e [2,6] come mostrato nel diagramma), puoi semplicemente procedere con la normale routine di unione per ottenere un array ordinato.

L'iterazione attraverso l'array e la generazione immediata dei sotto-array richiesti sono meno efficienti rispetto all'esecuzione dei passaggi di divisione nella loro interezza?

— Jimmy_Rustle
fonte

Correlato: cs.stackexchange.com/questions/77075/…

— Omar l'

Risposte:

La confusione deriva dalla differenza tra la descrizione concettuale dell'algoritmo e la sua implementazione .

Unire logicamente l'ordinamento è descritto come suddividere l'array in array più piccoli e quindi unirli nuovamente insieme. Tuttavia, "dividere l'array" non implica "creare un array completamente nuovo in memoria" o qualcosa del genere - potrebbe essere implementato nel codice come

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

cioè non ha luogo alcun lavoro reale e la "scissione" è puramente concettuale. Quindi quello che suggerisci sicuramente funziona, ma logicamente stai ancora "dividendo" le matrici - non hai bisogno di alcun lavoro dal computer per farlo :-)

— psmears
fonte

Personalmente mi piace molto il tipo di unione bottom up perché è più semplice da implementare in un modo che ti consente di evitare di allocare un buffer temporaneo ad ogni livello di ricorsione. Invece si alloca un buffer una volta e ping-pong tra di loro.

— maniaco del cricchetto

Questo divario è computazionalmente un no-op ... inoltre il suggerimento di OP è solo un'introduzione di un equivalente di una fusione di matrici a singolo elemento e iniziare a usare l'unione dal secondo passaggio, che sembra ridondante, perché anche l'unione originale funziona altrettanto bene. Non ha senso ottimizzarlo. Introduce solo concetti e logica ridondanti.

— luk32,

@ratchetfreak: lo adoro anche io, ma purtroppo non è equivalente al top-down (almeno la versione che conosco). Farà l'unione in modo diverso, sostanzialmente arrotondando alla successiva lunghezza dell'array power-of-2, che penso potrebbe anche essere un po 'più lenta. Conosci una versione bottom-up che fa esattamente le stesse fusioni senza pagare un costo elevato altrove?

— user541686

@Mehrdad l'unico vero problema è la piccola coda che deve essere unita. Nel peggiore dei casi ciò significa un altro passaggio da unire in un singolo articolo per matrici di lunghezza 1<<n+1. Anche se sono sicuro che puoi sistemare le cose in modo che una coda troppo piccola venga unita in un passaggio inferiore.

— maniaco del cricchetto

@psmears "semplicemente non hai bisogno di alcun lavoro dal computer per farlo" - quindi immagino che il costo delle prestazioni di n chiamate di qualche funzione di divisione ricorsiva (7 chiamate nel diagramma di esempio) sia sostanzialmente trascurabile?

— Jimmy_Rustle,

Immagino che cosa intendi per implementazione dal basso . Nell'implementazione dal basso si parte da singoli elementi di cella e si sposta verso l'alto unendo gli elementi in elenchi / array ordinati più grandi. Basta invertire le frecce nella figura sopra a partire dall'array centrale, ovvero array di un elemento.

Inoltre, potresti voler ottimizzare l'ordinamento di unione dividendo le matrici fino a quando non raggiungono una dimensione costante, dopodiché le puoi semplicemente ordinare usando, ad esempio, l'ordinamento per inserzione.

In caso contrario, l'ordinamento senza divisione dell'array non è possibile. In effetti l'essenza dell'ordinamento Merge sta dividendo e ordinando i subarrays, vale a dire, dividi e conquista.

— fade2black
fonte