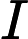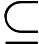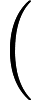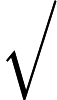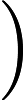NTIME (n ^ k) ≠ DTIME (n ^ k)?

33

In "Sul determinismo contro il non determinismo e problemi correlati" (Proc. IEEE FOCS, pagine 429–438, 1983), Paul, Pippenger, Szemerédi e Trotter hanno dimostrato che .
$\mathsf{NTIME}(n)\neq\mathsf{DTIME}(n)$

Questo risponde alla mia domanda con k = 1. Si sa qualcosa su un risultato simile per un altro k fisso?

cc.complexity-theory

— Bruno
fonte

26

Nessun limite inferiore incondizionato è noto per qualsiasi nel modello multitape TM (o per qualsiasi modello più forte di esso). $k \geq 2$

Ravi Kannan ha studiato questo problema in "Verso la separazione del determinismo dal determinismo" (1984) . Nel tentativo di mostrare è riuscito a provare quanto segue: esiste una costante universale tale che per ogni , . Qui, è la classe di linguaggi riconosciuta dalle macchine che usano contemporaneamente il tempo e lo spazio . Chiaramente ma non si sa se sono uguali. $NTIME(n^k) \neq TIME(n^k)$ $c \geq 1$ $k$ $NTIME(n^k) \not \subseteq TIME-SPACE(n^k,n^{k/c})$ $TIME-SPACE(n^k, n^{k/c})$ $n^k$ $n^{k/c}$ $TIME-SPACE(n^k,n^{k/c}) \subseteq TIME(n^k)$

Se si assume per alcuni $k \geq 2$ che $NTIME(n^k) = TIME(n^k)$ , si ottengono conseguenze interessanti. $P=NP$ è ovvio, ma implica anche che ${\sf NL} \neq {\sf P}$ . Ciò può essere dimostrato utilizzando un argomento "alternation-trading". Fondamentalmente, per ogni $k$ e ogni lingua $L \in {\sf NL}$ , c'è una costante $c$ e qualche macchina alternata che riconosce $L$ e fa alternanze $c$ , indovina $O(n)$ bit per alternanza, quindi passa a una modalità deterministica e viene eseguito in $n^k$ tempo. (Questo segue, ad esempio, dal giocare con le costruzioni inFortnow, "Time-Space Tradeoffs for Satisfiability" (1997) .) Ora se $TIME(n^k) = NTIME(n^k)$ allora tutte queste alternanze $c$ possono essere rimosse con solo una piccola quantità di overhead, e si finisce con un $TIME(n^k)$ calcolo che riconosce $L$ . Quindi ${\sf NL }\subseteq TIME(n^k) \neq {\sf P}$ . Probabilmente non esiste una simile simulazione alternata, ma se puoi escluderla, avrai il limite inferiore che cerchi. (Nota: credo che l'argomento sopra riportato sia anche nel documento di Kannan.)

— Ryan Williams
fonte

11

mentre non è esattamente quello che stai chiedendo, rj lipton nel suo blog commenta la difficoltà fondamentale dei risultati in questo settore e che l'approccio tipico del "padding" non si applica [1] e sottolinea che il risultato di PPST come citi è stato recentemente è stato leggermente esteso (da un fattore logaritmico) da Santhanam [2] cioè