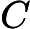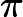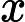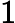Una nozione di circuiti quantistici monotoni

Nella complessità computazionale esiste un'importante distinzione tra calcoli monotone e generali e un famoso teorema di Razborov afferma che 3-SAT e persino MATCHING non sono polinomiali nel modello monotono dei circuiti booleani.

La mia domanda è semplice: esiste un analogo quantico per circuiti monotone (o più di uno)? Esiste un teorema quantistico di Razborov?

Stai davvero facendo due domande diverse e speri che ci sia una sola risposta che risponda ad entrambe: (1) Quali sono le nozioni naturali dei circuiti monotoni quantistici? (2) Come sarebbe un risultato quantico in stile Razborov basato su reticolo?

Non è ovvio come raggiungere entrambi allo stesso tempo, quindi descriverò ciò che a me sembra una nozione ragionevole di circuiti monotonici quantistici (senza indicare se esiste o meno un risultato Razborov corrispondente) e una nozione completamente diversa di che aspetto avrebbe una congettura quantistica "naturale" di Razborov (senza indicare se è probabile che sia vera).

Cosa vogliamo dal quantum

Come ho osservato nei commenti, penso che non sia necessario cercare di spremere la nozione di circuiti monotonici in uno stampo di unità. Sia nel fatto che l'evoluzione nel tempo non debba preservare la base standard, sia che esistano molteplici basi di misurazione in cui i risultati possono essere intrecciati, penso che la sine qua non del calcolo quantistico sia il fatto che il la base standard non è l'unica base. Anche tra gli stati del prodotto, in alcune implementazioni è definito solo da una scelta di frame di riferimento.

Ciò che dobbiamo fare è considerare le cose in modo tale da rimuovere la base standard dal suo tradizionale luogo privilegiato - o, in questo caso, il più possibile mantenendo una nozione significativa di monotonia.

Un semplice modello di circuiti monotoni quantistici

Si consideri un modello circuitale implicito nel commento di Tsuyoshi Ito sui "canali quantistici monotone" (e che è praticamente ciò che si deve fare se si desidera una nozione di "circuito" che non si limiti all'evoluzione unitaria).

Sia $\mathbf H$ lo spazio degli operatori eremiti su $\mathbb C^2$ (in modo che contenga tutti gli operatori di densità su un qubit). Come definiremmo una porta monotona quantistica $\mathsf G: \mathbf H_a \otimes \mathbf H_b \to \mathbf H_c$ da due qubit di input $a,b$ a un qubit di output $c$ , in modo tale che non sia effettivamente un gate monotono classico? 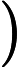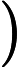Penso che sia semplice affermare che l'output non dovrebbe essere limitato a $|0\rangle\!\langle 0|$o$|1\rangle\!\langle 1|$o loro miscele; bu che per essere "monotono", dobbiamo obbligare i$\langle 1 | \,\mathop{\mathrm{Tr}_a}\bigl(\rho_{ab}\bigr) |1\rangle$e $\langle 1 | \,\mathop{\mathrm{Tr}_b}\bigl(\rho_{ab}\bigr) |1\rangle$incremento, il valore di$\langle 1 | \mathsf G(\rho_{ab}) | 1 \rangle$deve essere non decrescente. Per un gate a due qubit di input, ciò significa che$\mathsf G$deve essere implementabile in linea di principio come

1. eseguire una misurazione a due qubit rispetto ad alcune basi ortonormali $\{ |00\rangle, |\mu\rangle, |\nu\rangle, |11\rangle \}$ , dove $|\mu\rangle,|\nu\rangle$ coprire l'sottospazio di Hamming peso 1, e

2. producendo come output uno stato $\rho \in \{ \rho_{00}, \rho_\mu, \rho_\nu, \rho_{11} \}$ corrispondente al risultato misurato, dove per ogni .$\langle 1 | \rho_{00} | 1 \rangle \leqslant \langle 1 | \rho_\lambda | 1 \rangle \leqslant \langle 1 | \rho_{11} | 1 \rangle$$\lambda \in \{ \mu, \nu \}$

I circuiti sono solo composizioni di questi nel modo ragionevole. Potremmo anche consentire il fan-out, sotto forma di circuiti che incorporano e ; dovremmo almeno consentire queste mappe all'ingresso, per consentire a ciascun bit di ingresso (nominalmente classico) di essere copiato.$|0\rangle \mapsto |00\cdots 0\rangle$$|1\rangle \mapsto |11\cdots 1\rangle$

Sembra ragionevole considerare l'intero continuum di tali cancelli o limitarsi a una raccolta finita di tali cancelli. Ogni scelta dà origine a una "base quantistica monotona" diversa per i circuiti; si può considerare quali proprietà hanno diverse basi monotone. Gli stati possono essere scelti in modo completamente indipendente, soggetto al vincolo di monotonicità; sarebbe indubbiamente interessante (e probabilmente pratico limitare l'errore) impostaree, anche se non vedo alcun motivo per richiederlo nella teoria. Ovviamente AND e OR sono porte di questo tipo, dovee$\rho_{00}, \rho_\mu, \rho_\nu, \rho_{11}$$\rho_{00} = |0\rangle\!\langle 0|$$\rho_{11} = |1\rangle\!\langle 1|$$\rho_\mu = \rho_\nu = |0\rangle\!\langle 0|$$\rho_\mu = \rho_\nu = |1\rangle\!\langle 1|$rispettivamente, qualunque cosa si scelga o .$|\mu\rangle$$|\nu\rangle$

Per ogni costante k , si potrebbero anche considerare le basi del gate, comprese le porte k -input-one-output. L'approccio più semplice in questo caso sarebbe probabilmente quello di consentire a Gates che può essere implementato come sopra, consentendo qualsiasi decomposizione dei sottospazi di ogni peso di Hamming , e di richiedere che per ciascuno$\mathsf G: \mathbf H^{\otimes k} \to \mathbf H$$\mathcal V_w \leqslant \mathcal H_2^{\otimes k}$$0 \leqslant w \leqslant k$

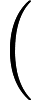
$$\max_{|\psi\rangle \in \mathcal V_w}\;\langle 1 | \,\mathsf G\Bigl( |\psi\rangle\!\langle\psi| \Bigr)\, |1\rangle \;\;\leqslant\;\; \min_{|\psi\rangle \in \mathcal V_{w+1}}\;\langle 1 | \,\mathsf G\Bigl( |\psi\rangle\!\langle\psi| \Bigr)\, |1\rangle$$ $0 \leqslant w < k$ . Non è chiaro quanta potenza computazionale aggiuntiva questo ti darebbe (nemmeno nel caso classico).

Non so se c'è qualcosa di interessante da dire su tali circuiti oltre al caso classico, ma questa mi sembra la definizione di candidato più promettente di un "circuito monotono quantistico".

Una variante quantistica del risultato di Razborov

Considera l' esposizione di Tim Gowers dei risultati di Alon & Boppana (1987), Combinatorica 7 pagg. 1–22 che rafforzano i risultati di Razborov (e rendono esplicite alcune delle sue tecniche) per la complessità monotona di CLIQUE. Gowers lo presenta in termini di costruzione ricorsiva di una famiglia di insiemi, a partire dagli " " del cubo booleano per ogni . Se rimuoviamo la posizione privilegiata della base standard nei set di basi, analogamente al Lemma locale Quantum Lovász , potremmo considerare un sottospazio di

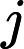
$$E_j = \Bigl\{ \mathbf x \in \{0,1\}^n \;:\; x_j = 1 \Bigr\}$$ $1 \leqslant j \leqslant n$$\mathcal H_2^{\otimes n}$corrispondere a una proposizione binaria (se uno stato appartiene al sottospazio o è invece ortogonale ad esso) che potrebbe derivare dalla misurazione. Ad esempio, possiamo considerare sottospazi dati da Permettiamo i quantum-logico analoghi di congiunzione e disgiunzione di sottospazi: $n$$\mathcal A_j \leqslant \mathcal H_2^{\otimes n}$ $$\begin{align*} \mathcal A_j = U_j \mathcal E_j \;, & \text{ for each $1 \leqslant j \leqslant n$} \\ \text{where } &\mathcal E_j := \Bigl\{ | \mathbf x \rangle \;:\; \mathbf x \in E_j \Bigr\} ; \\ &U_j : \mathcal H_2^{\otimes n} \to \mathcal H_2^{\otimes n} \text{ a unitary of bounded complexity}. \end{align*}$$ $$\begin{gather*} \mathcal A \wedge \mathcal B = \mathcal A \cap \mathcal B ; \\ \mathcal A \vee \mathcal B = \mathcal A + \mathcal B = \Bigl\{ \mathbf a + \mathbf b \,:\, \mathbf a \in \mathcal A\;,\; \mathbf b \in \mathcal B \Bigr\} . 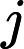\end{gather*}$$ Chiediamo quindi per quanto tempo è necessaria una costruzione ricorsiva di congiunzioni e disgiunzioni di spazi per ottenere uno spazio , in modo tale che il proiettore su differisca solo leggermente dal proiettore sullo spazio attraversato dalle funzioni indicatore di grafici aventi cricche di dimensione ; per esempio, in modo che$C$$\Pi_C$$C$$\Pi_{K(r)}$$r$$\| \Pi_C - \Pi_{K(r)} \|_\infty <\; 1/\mathrm{poly}(n)$. 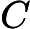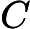La parte monotonica è coinvolta nelle operazioni logiche quantistiche e anche le proposizioni primitive sull'input sono quantistiche.

Nel caso generale, c'è un problema nel trattare questo come un problema computazionale: la disgiunzione non corrisponde a nessuna conoscenza che potrebbe essere ottenuta con certezza da misurazioni su un numero finito di copie usando misure in scatola nera per $\mathcal A$ e $\mathcal B$ da solo, a meno che non siano immagini di proiettori pendolari. Questo problema generale può ancora essere trattato come un risultato interessante sulla complessità geometrico-combinatoria e potrebbe dare origine a risultati relativi ai frustrati Hamiltionians locali. Tuttavia, potrebbe essere più naturale richiedere solo che i sottospazi $\mathcal A_j$derivano da proiettori pendolari, nel qual caso la disgiunzione è solo la classica OR dei risultati di misurazione di quei proiettori. Quindi potremmo richiedere che gli unitari siano tutti uguali, e questo diventa un problema su un circuito unitario (che dà origine agli "eventi primitivi") con post-elaborazione classica monotona (che esegue le operazioni logiche su quegli eventi).$U_j$

Si noti inoltre che se non imponiamo ulteriori restrizioni agli spazi , potrebbe trattarsi di un sottospazio con sovrapposizione molto elevata con dello spazio attraversato da stati di base standard , quali sono quelle stringhe binarie in cui .$\mathcal A_j$$\mathcal E_k^\bot$$\mathbf x \in \bar E_k$$x_k = 0$

• Se questa possibilità ti rende schizzinoso, puoi sempre richiedere che abbia un angolo di separazione da qualsiasi di almeno (in modo che i nostri sottospazi primitivi siano, nel peggiore dei casi, approssimativamente imparziali dai sottospazi in cui uno dei bit è impostato su 1).$\mathcal A_j$$\mathcal E_k^\bot$$\frac{\pi}{2} - 1/\mathrm{poly}(n)$

• Se non imponiamo tale restrizione, mi sembra che ammettere sottospazi con una sovrapposizione elevata con sarebbe comunque un ostacolo per approssimare CLIQUE (r); o saremmo più o meno limitati a considerare l' assenza di un bordo particolare (piuttosto che la sua presenza), o saremmo costretti a ignorare del tutto uno dei bordi. Quindi, non vedo che sia estremamente importante imporre alcuna restrizione a , tranne forse che sono tutte le immagini di un set di proiettori pendolari, se il proprio obiettivo è considerare come "valutare monotonicamente CLIQUE da semplici proposizioni quantiche ". Nel peggiore dei casi, equivarrebbe in modo classico a consentire le porte NOT all'ingresso (e che tutte le uscite di ventilazione si verifichino dopo la negazione).$\mathcal E_k^\bot$$\mathcal A_j$

Ancora una volta, non mi è chiaro se la sostituzione dei set di basi con sottospazi arbitrari di dia origine a un problema più interessante rispetto al semplice utilizzo dei sottospazi ; sebbene se ci limitassimo al caso delle formule CNF (sia nel caso pendolarismo che non pendolarismo), i risultati che otteniamo corrisponderebbero a qualche nozione di complessità di un hamiltoniano privo di frustrazione il cui stato fondamentale era costituito da una base standard stati che rappresentano cricche.$\mathcal H_2^{\otimes n}$$\mathcal E_j$

Come evidenziato dai commenti di Robin e Tsuyoshi, la nozione di circuiti monotoni sembra facilmente estendibile ai circuiti quantistici.

Per avere una definizione significativa del circuito monotono quantistico, dobbiamo scegliere un ordinamento su stati quantistici rispetto al quale è definita la monotonia. Classicamente un'opzione ragionevole (e una che conduce alla nozione normale di circuiti monotonici), è il peso di Hamming, ma consideriamo un ordinamento dato da una funzione arbitraria .$f$

Poiché l'evoluzione di un sistema quantistico chiuso è unitaria (che possiamo supporre sia data da ), allora per ogni stato tale che esiste uno stato alternativo tale che ma per il quale , e quindi l'evoluzione non è monotonica.$U$$|\psi\rangle$$f(U|\psi\rangle)>f(|\psi\rangle)$$|\phi\rangle$$f(|\phi\rangle) > f(|\psi\rangle)$$f(U|\psi\rangle)>f(U|\phi\rangle)$$U$

Quindi gli unici circuiti monotonici rispetto a sono quelli che per tutti . Pertanto, qualsiasi set di porte monotonico rispetto a è composto da porte che commutano con .$f$$f(U|\psi\rangle)=f(|\psi\rangle)$$|\psi\rangle$$f$$f$

Ovviamente, gli insiemi di porte che possono soddisfare questo dipendono dalla definizione di . Se è costante, tutti i set di porte sono monotonici rispetto ad essa. Tuttavia, se scegliamo come peso di Hamming degli stati nella base computazionale (un'estensione in qualche modo naturale della usata nel caso classico), otteniamo una struttura interessante. La restrizione imposta richiede che il peso di Hamming rimanga invariato. Le operazioni che mantengono questo importo in operazioni diagonali o SWAP parziali o combinazioni di queste. Questa struttura si presenta abbastanza spesso in fisica (in modelli a legame stretto ecc.), Ed è simile al problema di scattering del Bosone studiato da Aaronson e Arkhipov$f$$f$$f$$f$, sebbene non identico (è un problema di scattering leggermente diverso). Inoltre contiene circuiti per IQP e quindi non dovrebbe essere simulabile in modo efficiente in modo classico.

poni fondamentalmente due domande di difficoltà ampiamente divergenti, alla frontiera di due grandi campi, vale a dire circuiti booleani e informatica QM, sulla possibilità di quello che a volte viene chiamato un "teorema del ponte" in matematica:

• analogo quantico dei circuiti monotoni

• analogo quantico di Razborovs thm

la breve e candida risposta è no o non così lontana .

poiché (1), una domanda non così difficile, ma apparentemente ancora considerata raramente, ha rivelato il seguente riferimento che potrebbe essere preso come un caso correlato in letteratura.

Durezza di approssimazione per problemi quantistici di Gharibian e Kempe

considerano alcuni problemi "monotone" in un contesto quantico, ad esempio QMSA, "Quantum Monotone Minimum Satisfying Assignment, QMSA", ovvero un analogo SAT QM; (anche un altro problema Parola di peso minimo monotono quantico, QMW) e mostrano alcuni risultati di durezza di approssimazione, cioè limiti inferiori. non considerano i circuiti quantistici monotoni di per sé, ma un'idea potrebbe essere che un circuito quantistico o un algoritmo che risolva la funzione monotona QMSA può essere preso come un analogo QM.

quanto a (2) sarebbe un risultato molto avanzato se esistesse, che non sembra "finora". Il thm di Razborov è fondamentalmente un risultato di tipo "collo di bottiglia" con limite inferiore considerato una svolta distintiva e un risultato pressoché ineguagliabile nella teoria dei circuiti (monotona).

in modo approssimativo sì, certo, ci sono alcuni colli di bottiglia nel limite inferiore che si trovano nell'informatica QM, ad esempio relativi a teoremi di prodotto diretti, per un sondaggio vedi ad es.

Algoritmi quantistici, limiti inferiori e compromessi spazio-tempo di Spalek

tuttavia, probabilmente un limite inferiore di calcolo QM analogo migliore metterebbe un limite inferiore sul numero di operazioni qubit o eventualmente basato su porte "complete" come porte Toffoli per una funzione monotona. non sono a conoscenza di prove di questo tipo.

un altro approccio potrebbe limitare l'analisi a speciali porte quantiche AND e OR con ulteriori bit "ancilla" aggiunti per rendere reversibili le porte.