Come descrivere la rotazione delle estremità opposte di un corpo a causa di un momento applicato

Sommario

Un modo breve per formulare questa domanda è:
Shear descrive la traduzione di una parte di un corpo rispetto a un'altra data una forza applicata.
Qual è il termine rotazionale equivalente? Questo è,

Cosa descrive la rotazione di una parte di un corpo rispetto a un'altra, dato un momento di forza applicato?

Più in dettaglio:

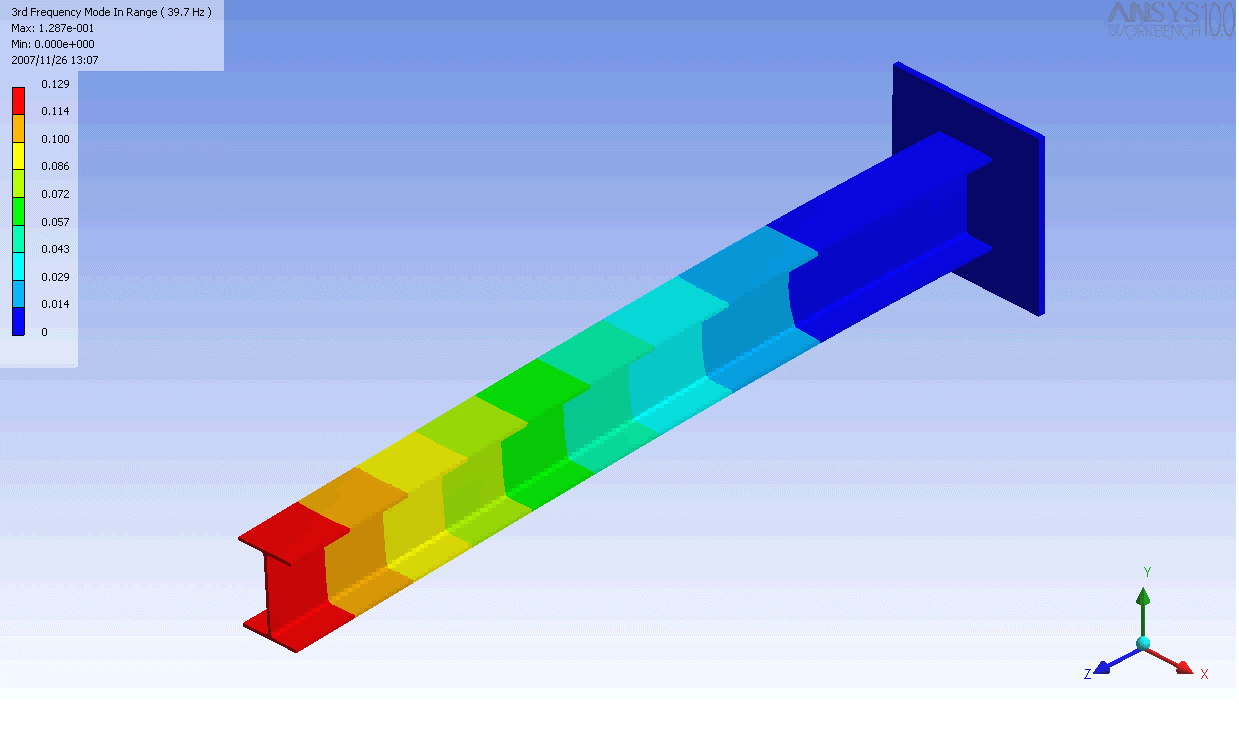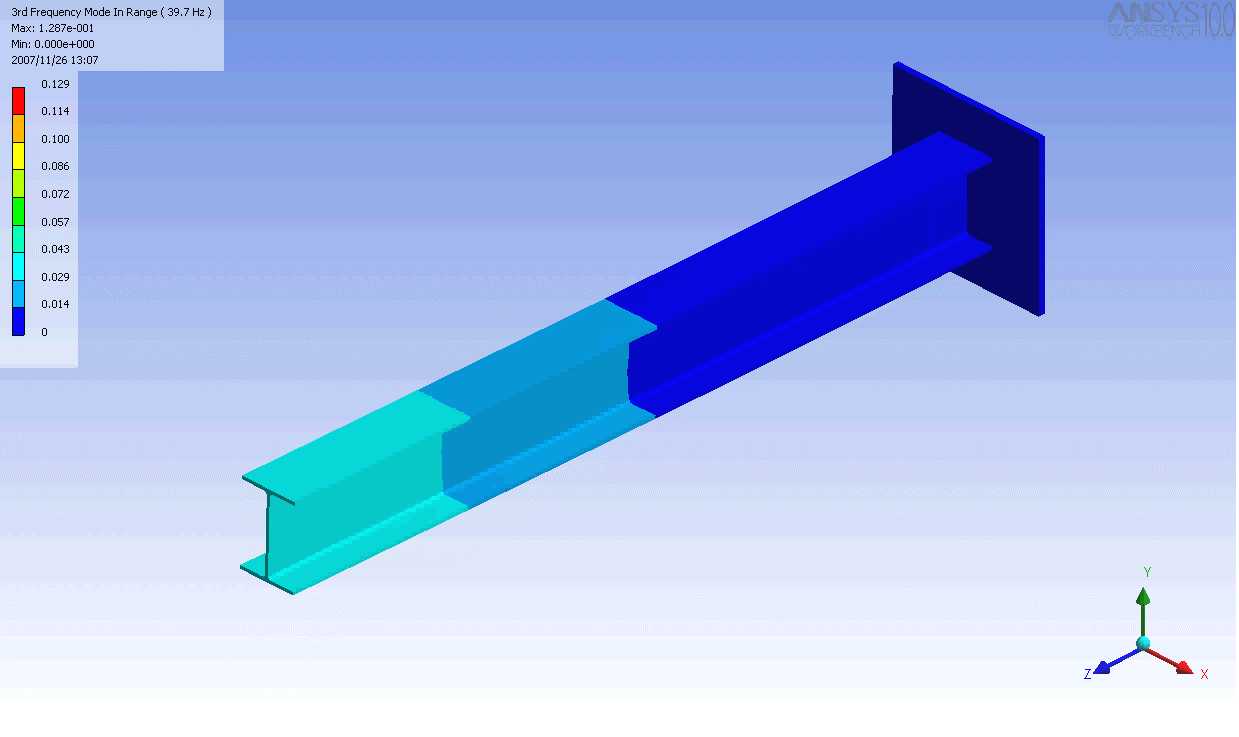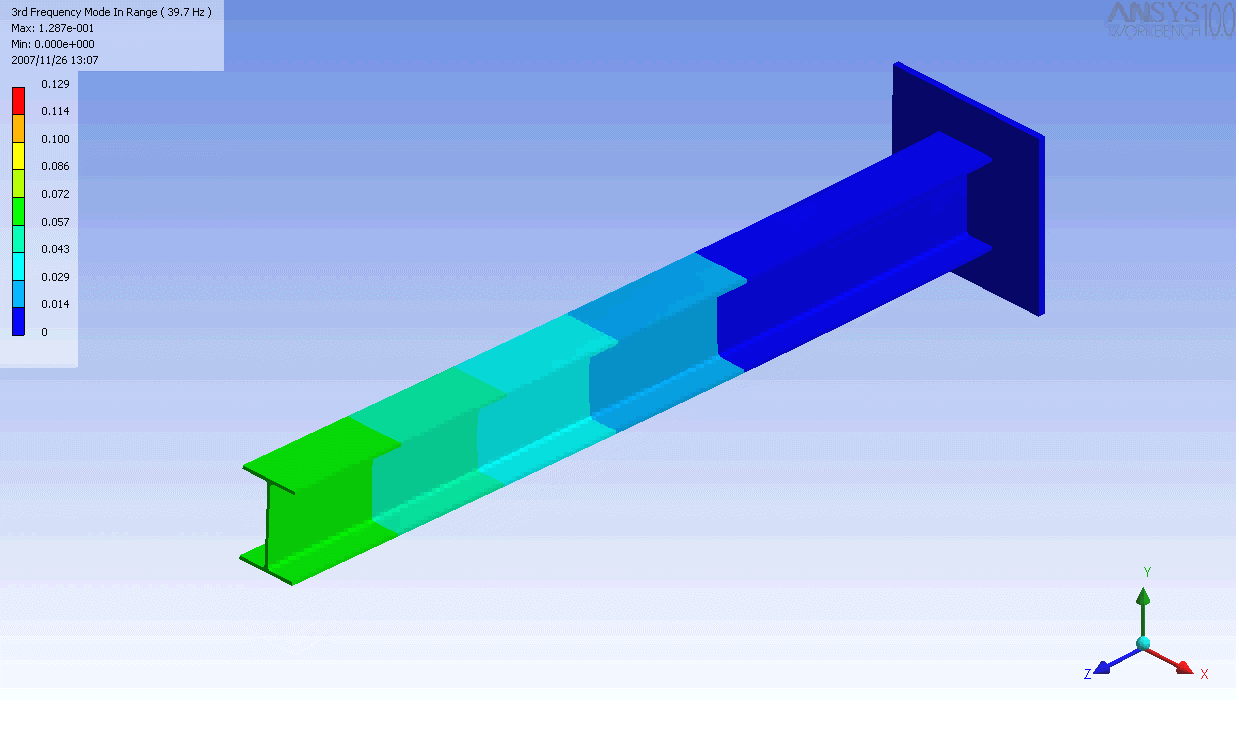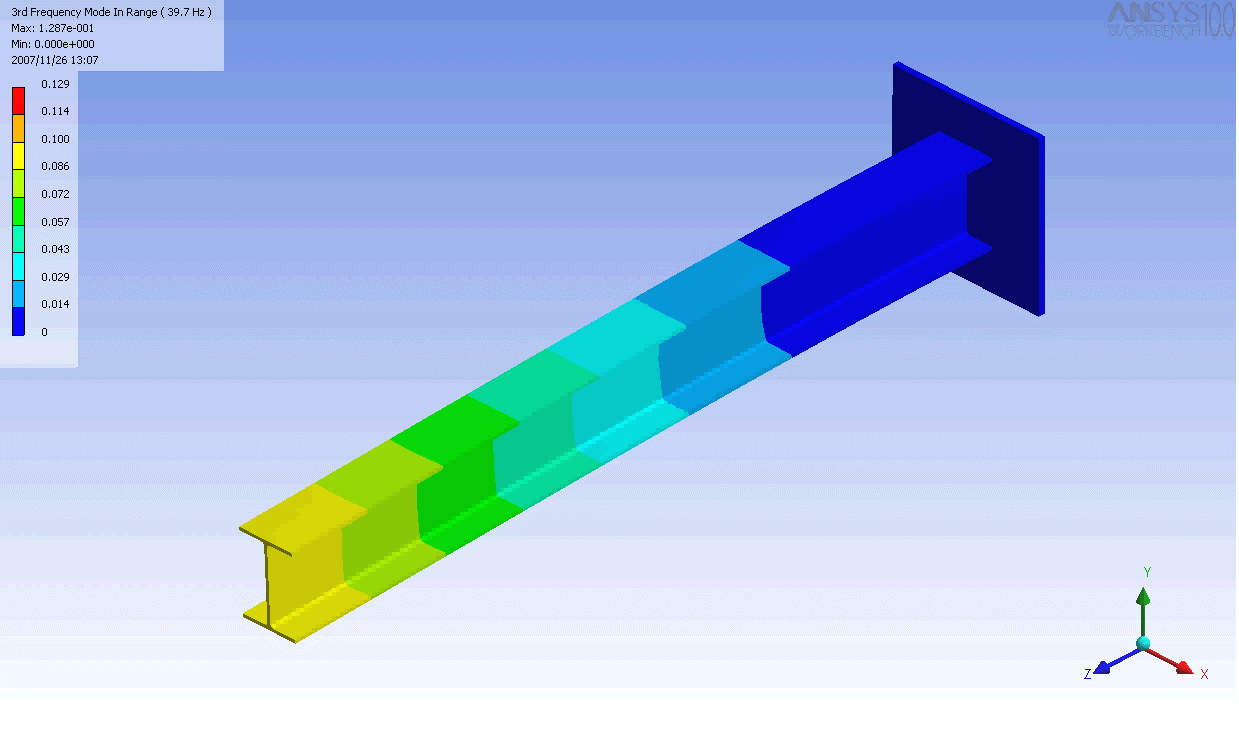
Sto cercando di trovare la parola giusta per un particolare tipo di distorsione. Ho un assieme di elementi collegati per essere approssimativamente solido. Ne monto uno piatto a una parete e metto un po 'di forza o momento sul lato piatto opposto in modo che il gruppo si distorca. In particolare, desidero descrivere correttamente la rotazione relativa dei due piani (in qualsiasi direzione) e desidero che questo termine descriva solo la rotazione ed escluda qualsiasi traduzione (in modo che se si taglia solo senza torcere mi piacerebbe quantità da zero).

Ho pensato alla torsione , ma le definizioni di torsione sembrano sempre riferirsi a una barra o ad un asse allungato di qualche tipo. È necessaria una barra affinché la "torsione" sia significativa? Ho pensato alla torsione , ma ciò non implica necessariamente una quantità dinamica, quindi, ad esempio, si potrebbe congelare in una torsione e qualcosa può essere contorto senza applicare forze. Non credo che bend sia corretto perché potrebbe riferirsi solo alla traduzione. C'è una parola migliore a cui non sto pensando, o anche una frase concisa?

Se esiste una parola che soddisfa le mie esigenze, un riferimento che potrei rivedere sarebbe molto utile.

Perché "piegare" non è la parola di cui ho bisogno

Di seguito è riportato uno schizzo di due oggetti che si piegano lungo la stessa curva (sia per intuizione che per equazioni), tuttavia la rotazione delle estremità è diversa in ciascuna. Sono interessato a una parola o una frase per descrivere la rotazione delle estremità (o una tendenza delle estremità a ruotare o no, ecc.).

Inoltre, secondo Wikipedia, la flessione "caratterizza il comportamento di un sottile elemento strutturale" sotto carico, ma non mi interessano gli elementi sottili (e ho solo disegnato quanto sopra per illustrare la flessione). Il primo è il modo comune in cui un raggio si piegherebbe, ma non tutto si piega come un raggio, e spero di trovare una parola che caratterizzi la particolare differenza qui illustrata.

Cose che non si piegano come normali raggi

Un modello ragionevole è un materiale altamente anisotropico, rigido su un asse ma meno negli altri. Ad esempio, un fascio di cavi in ​​fibra ottica paralleli.

Penso che un altro sarebbe un tubo pieno d'acqua ad alta pressione, come una manichetta antincendio. (Non so come questo si pieghi, ma dubito che si pieghi come un raggio.)

Ecco uno schizzo di una struttura che non si piega come una trave, in quanto il lato parallelo al muro rimane parallelo, anche se il resto della struttura si piega in modo normale. I punti neri hanno lo scopo di rappresentare i giunti rotanti. Anche se questo oggetto fosse lungo e snello, penso che le estremità rimarrebbero parallele. Il punto della terza immagine è che non devi necessariamente vedere cosa c'è dentro (ma potrebbe essere comunque importante descrivere che le due pareti non ruotano l'una rispetto all'altra in risposta a una forza applicata).

Quello che stai descrivendo è un sottoinsieme del concetto generale di rigidità (o rigidità). Penso che la misura che stai cercando sia l'inverso della rigidità rotazionale ( come definita da Wikipedia ):

$$k=\frac {M} {\theta}$$

M è il momento applicato
θ è la rotazione

Si potrebbe dire qualcosa del tipo: "La rigidità rotazionale dell'assieme è molto elevata, in modo tale che la rotazione dell'estremità libera con un momento flettente applicato è quasi zero".

Se hai bisogno di trovare un termine per l'inverso della rigidità rotazionale, potresti ottenere un po 'di chilometraggio da "inclinazione", come in "L'estremità dell'assieme opposta e parallela alla parete non tenderà ad inclinarsi rispetto a il muro quando viene applicata una forza. "

Informalmente, questo uso di "skew" può avere senso per il lettore; formalmente, è un po 'complicato da giustificare e un pubblico di ingegneri potrebbe indovinarlo. Si potrebbe obiettare che ci sono più linee parallele tra piani paralleli di quante ce ne siano tra piani intersecanti, poiché tutte le linee parallele tra piani intersecanti devono essere parallele alla linea di intersezione, pertanto i piani intersecanti sono più "inclinati" perché ci sono meno modi per accoppiare linee tra loro che non sono inclinate. Saresti comunque su un terreno instabile con i matematici.

Questa è la mia risposta diretta alla tua domanda sul vocabolario / documentazione. Il resto sarà un po 'più libero, a partire da una risposta al tuo commento sulla risposta di AndyT :

il mio assemblaggio non ha davvero superfici chiare (pensa a due sfere attaccate insieme). Quindi, invece di, diciamo, "rigidità torsionale", avrei bisogno di qualcosa del tipo "date due superfici virtuali, una vicino alla superficie di rilegatura e una vicino all'estremità libera, quando viene applicata una forza all'estremità libera, i due le superfici virtuali subiranno solo una piccola rotazione relativa ".

Dovrai almeno definire inizialmente queste superfici virtuali. Uno di questi dovrebbe essere facile, dal momento che è un piano definito da un muro. Se il muro è curvo, è possibile utilizzare il piano con un vettore normale che calcola la media degli assi dei dispositivi di fissaggio utilizzati per montare il gruppo, che passa attraverso un "centroide di montaggio" (chiamarlo "muro virtuale" se lo si desidera). Una geometria più complessa richiederà una spiegazione più complessa; gli sforzi per ridurre la complessità di tale spiegazione sono irragionevoli se e quando compromettono l'efficacia della spiegazione.

Travi e alberi a parte, la differenza tra rigidità rotazionale e rigidità torsionale ha a che fare con la natura delle forze applicate. La rigidità rotazionale corrisponde ai momenti flettenti, mentre la rigidità torsionale corrisponde ai momenti torcenti; in un contesto torsionale, i tuoi piani virtuali sarebbero piani di rotazione . Lo stesso non sarebbe vero in un contesto flettente.

Per un'analogia, considera il movimento di un cubo di Rubik . Quando si torce uno degli strati del cubo, l'angolo attraverso il quale si sposta lo strato è all'interno del piano del cubo. Ora, immagina di attorcigliare un grumo di gomma delle dimensioni di una palla da softball nello stesso modo in cui ruoteresti un cubo di Rubik. Poiché la gomma è solida, la metà in una mano è vincolata rispetto alla metà nell'altra mano e nel momento in cui la si applica la deforma. Quanto si deforma dipende dalla sua rigidità torsionale ; le sollecitazioni interne sono sollecitazioni di taglio.

Allo stesso modo, considera il movimento di una fisarmonica. Le due estremità della fisarmonica sono inizialmente parallele ma, quando si tiene la fisarmonica tra le due mani, è possibile manipolarla in modo che le estremità non siano parallele (a causa del suo diaframma flessibile). Ora ricorda quel grumo di gomma. Tenendolo nella stessa impugnatura di prima, è possibile applicare un momento flettente per deformare la gomma in modo diverso, corrispondente alla flessione anziché alla torsione. Quanto si deforma ora dipende dalla sua rigidità rotazionale ; le sollecitazioni interne sono normali.

Se abbiamo una trave o un albero snello, la torsione è praticamente rilevante solo rispetto a un singolo asse e la flessione è praticamente solo rilevante rispetto agli altri due (cioè gli assi maggiore e minore di una trave). Se abbiamo un grumo di gomma, potrebbero verificarsi flessione e torsione che potrebbero essere significative in qualsiasi direzione. Non abbiamo il vantaggio di semplici equazioni sviluppate per travi e alberi classici (o anche metodi meno semplici usati per, ad esempio, travi corte), ma "torsione" e "flessione" sono ancora significativi.

$\theta$$M$$\theta \approx 0°$

Ricordare, se si incontra il problema di definire formalmente piani virtuali, i punti fissati al piano quando l'assemblaggio viene scaricato devono rimanere collineari in modo che il piano virtuale non si deformi in una superficie curva durante il caricamento. (Vuoi misurare l'angolo tra le superfici curve? Io no!)

Nella teoria del raggio di Eulero-Bernoulli , questo è noto come flessione , o, se il "raggio" continua a oscillare, flessione dinamica .

In questo caso specifico - supponendo che "su" sia "su" nella vita reale - questa è chiamata la prima flessione verticale . Viene mostrato dinamicamente qui:

I termini alternativi includono deflessione (data qui ) e azione di piegatura (data qui ), anche se sono meno sicuro dell'applicabilità di quest'ultimo.

Prima immagine

Se capisco correttamente l'immagine e la spiegazione, stai cercando una parola per descrivere il passaggio da "A" a "A + dA". Nel qual caso la parola che ti serve, in senso generico, è rotazione .

Se vuoi qualcosa di più specifico per la tua situazione particolare, stai cercando la rotazione di un piano rispetto a un altro .

Ridicolmente, dopo aver scritto e riletto la domanda originale, nella descrizione viene effettivamente utilizzata la rotazione relativa ! C'è qualche motivo per cui non pensavi fosse il termine corretto?

Seconda foto

Le travi superiore e inferiore nella parte centrale sono flesse . Per la struttura complessiva le sezioni del piano non sono rimaste piane . Ciò prenderebbe la descrizione generalizzata della distorsione .

Sommario

Hai chiesto: cosa descrive la rotazione di una parte di un corpo rispetto a un'altra data una coppia applicata? La risposta semplice, generica, è distorsione . Ma stai complicando le cose guardando un corpo piuttosto che un membro . Per un membro , la rotazione causata da un momento è, semplicemente, flettente . Ma hai rifiutato questo perché stai guardando una struttura più grande che ha complicate rigidità relative ecc. Ciò significa che perdi le belle parole precise e devi invece fare affidamento su quelle generiche. Ecco perché la distorsione è probabilmente la più accurata, ma non specifica della rotazione.