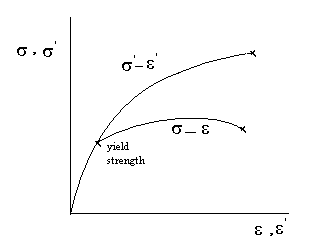Perché usiamo persino lo stress ingegneristico?

Sorprendentemente questo non è stato chiesto prima, quindi mi manca qualcosa di semplice.

Usiamo lo stress ingegneristico e la tensione ingegneristica in questo eq. Stress = (modulo di Young) × (sforzo). Questo eq. viene utilizzato nell'analisi delle travi di curvatura, degli alberi di torsione e nella deformazione. Quindi l'equazione finale di flessione e torsione darà noi valore dello stress ingegneristico ma non il valore dello stress.$(\frac{M}{I} = \frac{\sigma}{y})$$(\frac{T}{I} = \frac{\tau}{r})$

Perché stiamo prendendo in considerazione lo stress ingegneristico invece del vero stress mentre sappiamo che non darà il corretto valore dello stress?

Alcune cose che ho letto sono:

1. Difficile da misurare.
2. Non c'è molta differenza e possiamo semplicemente applicare un fattore di sicurezza.
3. "Non riteniamo che i materiali cambino la loro sezione trasversale dopo il caricamento, poiché progettiamo di non avere deformazioni plastiche la regione elastica è più importante, quindi ciò che accade dopo il limite proporzionale non è importante"

In primo luogo, 1 e 2 non sono ragioni reali per me. Il numero 3 sembra plausibile dal momento che progettiamo sempre nella regione elastica, ma è questo? La tensione ingegneristica fornisce anche informazioni valide dopo il limite proporzionale?

Usiamo la deformazione ingegneristica anche se non è il valore "corretto" perché nella maggior parte dei casi, in particolare nel regime elastico, la deformazione ingegneristica differisce in modo trascurabile dalla deformazione reale.

Per i materiali elastici lineari, hookean, generalmente la tensione del case sul limite elastico è molto ridotta. Anche gli acciai più forti, ad esempio, hanno un limite superiore quando si lavora a freddo di circa . Il modulo di acciaio è circa . Pertanto per gli acciai più forti. Quindi all'inizio della deformazione plastica, la deformazione ingegneristica è dello . Molti materiali elastici utili hanno una tensione ingegneristica molto più bassa ai loro limiti elastici.$\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$$E=200\times 10^{9}\ \textrm{Pa}$$\varepsilon_{\textrm{el}}=0.005=0.5\%$$0.5\%$

Per un solido elastico isotropico, hookean, vale quanto segue

$$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$$

senza perdita di generalità nella scelta di . Quindi, in tensione uniassiale al limite elastico, supponendo che il materiale sia libero di contrarsi. Pertanto . Poiché il rapporto di Poisson è circa 0,3 per gli acciai in regime elastico, la deformazione di compressione lineare trasversale è . L'area della sezione trasversale al limite elastico è quindi , o molto vicino a volte l'area originale. σ x 2 = σ x 3 = 0 ε x 2 = ε x 3 = - σ el$x_{i}$$\sigma_{x_{2}}=\sigma_{x_{3}}=0$ν0,0015(1-0,0015)2A0$\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$$\nu$$0.0015$$(1-0.0015)^{2}A_{0}$$0.997$

Quindi la vera deformazione è volte più grande della deformazione ingegneristica al limite elastico, o circa volte, o circa più grande. Tieni presente che questo è al limite elastico di un materiale linearmente elastico eccezionalmente forte, e quindi è una stima ragionevolmente conservativa della differenza tra sforzo reale e sforzo ingegneristico nel regime elastico. 1,0030,3$\frac{1}{0.997}$$1.003$$0.3\%$

Mentre l'analisi sopra è ragionevolmente utile per i solidi Hookean linearmente elastici, non è altrettanto valida per polimeri e materiali biologici. Tali materiali sono generalmente viscoelastici (o completamente un'altra classe di materiale) e quindi obbediscono a regole diverse nel loro comportamento. La vera deformazione inoltre differisce abbastanza selvaggiamente dalla deformazione ingegneristica nel regime plastico, come evidenziato nel seguente diagramma (trovato qui )

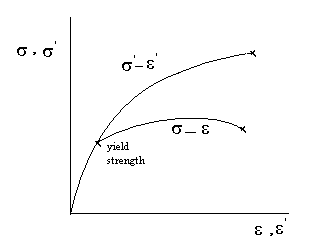
Per quanto riguarda i tuoi punti:

1. Misurare i cambiamenti nell'area della sezione trasversale durante la deformazione è difficile. Richiede un posizionamento accurato della strumentazione calibrata su campioni di prova lavorati con precisione. Si potrebbero usare gli estensimetri posti ai lati di una barra di trazione per misurare la deformazione laterale in tensione uniassiale e compressione nelle apparecchiature di prova di trazione . Ottenere risultati statisticamente significativi richiede molti campioni, oltre a tempi, sforzi e costi significativi.

2. Non v'è poca differenza. Spero di aver adeguatamente spiegato sopra quanto piccola sia la differenza: ho calcolato una differenza di circa lo in un caso conservativo.$0.3\%$

3. L'idea che possiamo ignorare qualsiasi cosa oltre la fine del regime elastico, o che progettiamo sempre per il regime elastico, non è vera. La deformazione plastica può spesso valere la pena studiare. La modellazione di processi continui di formatura di forme come laminazione, disegno, estrusione, ecc. Richiede una profonda comprensione della meccanica della deformazione plastica per funzionare correttamente e, a tal fine, la vera sollecitazione e la vera tensione sono inestimabili. In particolare per la trafilatura, vedere (questo pdf ) e trovare l'equazione 7. La deformazione plastica è utile anche per la modellazione di materiali che devono deformarsi permanentemente in alcuni casi d'uso previsti, come pannelli della carrozzeria e componenti del telaio durante una collisione. La deformazione plastica è utile perché assorbe energia cinetica.

Modifica: mi scuso, in realtà non ho risposto alla domanda di stress. Tuttavia, dovrebbe essere abbastanza chiaro che gli stessi punti si applicano allo stress come si applicano alla deformazione data la loro relazione lineare nel regime elastico. Ancora una volta, nel regime plastico, ci possono essere grandi variazioni.

Aggiungendo alla risposta di @ starrise:

Per quanto riguarda il licenziamento dei motivi 1 e 2, ti stai dimenticando di prendere in considerazione l'analisi costi-benefici che li riguarda. Come mostrato da @starrise nella loro risposta, la differenza di solito non è sostanziale (sebbene altri materiali di solito presentino differenze maggiori).

D'altra parte, i materiali mostrano sempre variazioni intrinseche dei loro valori. Il modulo di elasticità dell'acciaio ha un intervallo definito in diversi articoli da [a] a [b] (per l'intervallo di confidenza al 95%).± 15 $\pm6\%$ $\pm15\%$

Quindi, qual è il punto di considerare la vera tensione nella pratica ingegneristica di tutti i giorni se tutte le altre proprietà (tra cui la resistenza allo snervamento e le dimensioni della sezione trasversale) avranno fluttuazioni casuali che sono quasi sicuramente in grado di eliminare "l'errore" a causa dell'uso di sforzo ingegneristico anziché vero sforzo?