Separa i poligoni in base all'intersezione usando PostGIS

Ho una tabella di poligoni PostGIS in cui alcuni si intersecano. Questo è quello che sto cercando di fare:

• Per un dato poligono selezionato da id, dammi tutti i poligoni che si intersecano. Fondamentalmente,select the_geom from the_table where ST_Intersects(the_geom, (select the_geom from the_table where source_id = '123'))
• Da questi poligoni, devo creare un nuovo poligono in modo tale che l'intersezione diventi un nuovo poligono. Quindi se il poligono A si interseca con il poligono B, otterrò 3 nuovi poligoni: A meno AB, AB e B meno AB.

Qualche idea?

Dato che hai detto di ottenere un gruppo di poligoni che si intersecano per ogni poligono a cui sei interessato, potresti voler creare quello che viene chiamato "overlay poligonale".

Questo non è esattamente ciò che sta facendo la soluzione di Adam. Per vedere la differenza, dai un'occhiata a questa immagine di un incrocio ABC:

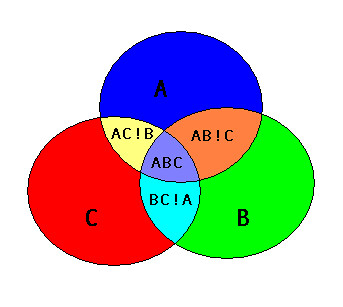
Credo che la soluzione di Adam creerà un poligono "AB" che copre sia l'area di "AB! C" e "ABC", sia un poligono "AC" che copre "AC! B" e "ABC", e un " BC "poligono che è" BC! A "e" ABC ". Quindi i poligoni di output "AB", "AC" e "BC" si sovrappongono all'area "ABC".

Una sovrapposizione di poligoni produce poligoni non sovrapposti, quindi AB! C sarebbe un poligono e ABC sarebbe un poligono.

La creazione di un overlay poligonale in PostGIS è in realtà piuttosto semplice.

Ci sono sostanzialmente tre passaggi.

Il passaggio 1 è quello di estrarre le linee [Nota che sto usando l' anello esterno del poligono, diventa un po 'più complicato se vuoi gestire correttamente i fori]:

SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines

Il passaggio 2 consiste nel "nodo" della linea (produrre un nodo ad ogni intersezione). Alcune librerie come JTS hanno classi "Noder" che puoi usare per farlo, ma in PostGIS la funzione ST_Union lo fa per te:

SELECT ST_Union(the_geom) AS the_geom FROM (...your lines...) AS noded_lines

Il passaggio 3 è creare tutti i possibili poligoni non sovrapposti che possono provenire da tutte quelle linee, fatto dalla funzione ST_Polygonize :

SELECT ST_Polygonize(the_geom) AS the_geom FROM (...your noded lines...)

È possibile salvare l'output di ciascuno di questi passaggi in una tabella temporanea oppure combinarli tutti in un'unica istruzione:

CREATE TABLE my_poly_overlay AS
SELECT geom FROM ST_Dump((
    SELECT ST_Polygonize(the_geom) AS the_geom FROM (
        SELECT ST_Union(the_geom) AS the_geom FROM (
            SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines
        ) AS noded_lines
    )
)

Sto usando ST_Dump perché l'output di ST_Polygonize è una raccolta di geometrie ed è (di solito) più conveniente avere una tabella in cui ogni riga è uno dei poligoni che compongono la sovrapposizione di poligoni.

Se ho capito bene, vuoi prendere (A è la geometria sinistra, B è la destra):

Immagine di A∪B http://img838.imageshack.us/img838/3996/intersectab1.png

Ed estrarre:

Un ∖ AB

Immagine di A ∖ AB http://img830.imageshack.us/img830/273/intersectab2.png

AB

Immagine di AB http://img828.imageshack.us/img828/7413/intersectab3.png

e B ∖ AB

Immagine di B ∖ AB http://img839.imageshack.us/img839/5458/intersectab4.png

Cioè - tre diverse geometrie per ogni coppia intersecante.

Innanzitutto, creiamo una vista di tutte le geometrie che si intersecano. Supponendo che il nome della tua tabella sia polygons_table, utilizzeremo:

CREATE OR REPLACE VIEW p_intersections AS    -- Create a view with the 
SELECT t1.the_geom as t1_geom,               -- intersecting geoms. Each pair
       t2.the_geom as t2_geom                -- appears once (t2.id<t2.id)
    FROM polygons_table t1, polygons_table t2  
         WHERE t1.id<t2.id AND t1.the_geom && t2.the_geom 
                           AND intersects t1.the_geom, t2.the_geom;

Ora abbiamo una vista (praticamente una tabella di sola lettura) che memorizza coppie di geomi che si intersecano, in cui ogni coppia appare solo una volta a causa della t1.id<t2.idcondizione.

Ora cerchiamo di raccogliere i vostri incroci - A∖AB, ABe B∖AB, usando SQL di UNIONsu tutti e tre domande:

--AB:
SELECT ST_intersection(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION 

--A∖AB:
SELECT ST_Difference(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION

--B∖AB:
SELECT ST_Difference(t2.the_geom, t1.the_geom) 
    AS geom 
    FROM p_intersections;

Gli appunti:

1. L' &&operatore viene utilizzato come filtro prima intersectsdell'operatore, per migliorare le prestazioni.
2. Ho scelto di creare una VIEWquery gigantesca anziché una; Questo è solo per comodità.
3. Se intendevi ABdire unione, non intersezione, di Ae B- Usa ST_Union invece di st_intersection nella UNIONquery nei punti appropriati.
4. Il ∖segno è un segno unicode per Imposta differenza; rimuoverlo dal codice se confonde il database.
5. Immagini per gentile concessione della bella categoria della teoria degli insiemi di Wikimedia Commons .

Quello che stai descrivendo è il modo in cui l' operatore Union lavora in ArcGIS, ma è un po 'diverso da Union o Intersection nel mondo GEOS. Il manuale di Shapely contiene esempi di come funzionano i set in GEOS . Tuttavia, il wiki di PostGIS ha un buon esempio usando il linework che dovrebbe fare al caso tuo.

In alternativa, potresti calcolare tre cose:

1. ST_Intersection (geom_a, geom_b)
2. ST_Difference (geom_a, geom_b)
3. ST_Difference (geom_b, geom_a)

Questi dovrebbero essere i tre poligoni che hai citato nel tuo secondo punto elenco.

Qualcosa di simile a:

INSERISCI IN new_table VALUES ((seleziona id, the_geom da old_table dove st_intersects (the_geom, (seleziona the_geom da old_table dove id = '123')) = true

MODIFICA: è necessaria l'intersezione effettiva del poligono.

INSERT INTO valori new_table ((seleziona id, ST_Intersection (the_geom, (seleziona the_geom dalla vecchia dove id = 123))

vedere se funziona.