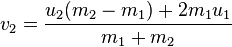Collisione da palla a palla - Rilevazione e manipolazione

Con l'aiuto della comunità Stack Overflow ho scritto un simulatore di fisica piuttosto semplice ma divertente.

Fai clic e trascina il mouse per lanciare una palla. Rimbalzerà intorno e alla fine si fermerà sul "pavimento".

La mia prossima grande caratteristica che voglio aggiungere è la collisione palla a palla. Il movimento della palla è suddiviso in vettore di velocità ascia e y. Ho gravità (piccola riduzione del vettore y ogni passo), ho attrito (piccola riduzione di entrambi i vettori ogni collisione con un muro). Le palle si muovono onestamente in modo sorprendentemente realistico.

Immagino che la mia domanda abbia due parti:

1. Qual è il metodo migliore per rilevare la collisione palla a palla?
   Ho solo un ciclo O (n ^ 2) che scorre su ogni palla e controlla ogni altra palla per vedere se il suo raggio si sovrappone?
2. Quali equazioni utilizzo per gestire le collisioni palla-palla? Fisica 101 In che
   modo influiscono sui vettori x / y delle due sfere? Qual è la direzione risultante in cui si dirigono le due palle? Come posso applicarlo a ogni palla?

Gestire il rilevamento delle collisioni delle "pareti" e i risultanti cambiamenti del vettore sono stati facili ma vedo più complicazioni con le collisioni palla-palla. Con i muri dovevo semplicemente prendere il negativo del vettore x o y appropriato e andava nella direzione corretta. Con le palle non penso che sia così.

Alcuni rapidi chiarimenti: per semplicità sto bene con una collisione perfettamente elastica per ora, anche tutte le mie palle hanno la stessa massa in questo momento, ma potrei cambiarlo in futuro.

Modifica: risorse che ho trovato utili

Fisica della sfera 2d con vettori: collisioni bidimensionali senza trigonometria.pdf
Esempio di rilevamento della collisione con sfera 2d: aggiunta del rilevamento delle collisioni

Successo!

Il rilevamento e la risposta della collisione con la palla funzionano alla grande!

Codice rilevante:

Rilevazione di collisioni:

for (int i = 0; i < ballCount; i++)  
{  
    for (int j = i + 1; j < ballCount; j++)  
    {  
        if (balls[i].colliding(balls[j]))  
        {
            balls[i].resolveCollision(balls[j]);
        }
    }
}

Questo controllerà le collisioni tra ogni palla ma salterà i controlli ridondanti (se devi controllare se la palla 1 si scontra con la palla 2, non dovrai controllare se la palla 2 si scontra con la palla 1. Inoltre, salta il controllo delle collisioni con se stessa ).

Quindi, nella mia classe di palla ho i miei metodi colliding () e resolCollision ():

public boolean colliding(Ball ball)
{
    float xd = position.getX() - ball.position.getX();
    float yd = position.getY() - ball.position.getY();

    float sumRadius = getRadius() + ball.getRadius();
    float sqrRadius = sumRadius * sumRadius;

    float distSqr = (xd * xd) + (yd * yd);

    if (distSqr <= sqrRadius)
    {
        return true;
    }

    return false;
}

public void resolveCollision(Ball ball)
{
    // get the mtd
    Vector2d delta = (position.subtract(ball.position));
    float d = delta.getLength();
    // minimum translation distance to push balls apart after intersecting
    Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d); 


    // resolve intersection --
    // inverse mass quantities
    float im1 = 1 / getMass(); 
    float im2 = 1 / ball.getMass();

    // push-pull them apart based off their mass
    position = position.add(mtd.multiply(im1 / (im1 + im2)));
    ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));

    // impact speed
    Vector2d v = (this.velocity.subtract(ball.velocity));
    float vn = v.dot(mtd.normalize());

    // sphere intersecting but moving away from each other already
    if (vn > 0.0f) return;

    // collision impulse
    float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
    Vector2d impulse = mtd.normalize().multiply(i);

    // change in momentum
    this.velocity = this.velocity.add(impulse.multiply(im1));
    ball.velocity = ball.velocity.subtract(impulse.multiply(im2));

}

Codice sorgente: fonte completa per il collettore palla a palla.

Se qualcuno ha qualche suggerimento su come migliorare questo simulatore di fisica di base fammelo sapere! Una cosa che devo ancora aggiungere è il momento angolare, quindi le palle rotoleranno in modo più realistico. Altri suggerimenti? Lascia un commento!

Per rilevare se due sfere si scontrano, basta controllare se la distanza tra i loro centri è inferiore a due volte il raggio. Per fare una collisione perfettamente elastica tra le sfere, devi solo preoccuparti del componente della velocità che è nella direzione della collisione. L'altro componente (tangente alla collisione) rimarrà lo stesso per entrambe le sfere. È possibile ottenere i componenti della collisione creando un vettore unitario che punta nella direzione da una palla all'altra, quindi prendendo il prodotto punto con i vettori di velocità delle palle. È quindi possibile collegare questi componenti in un'equazione di collisione perfettamente elastica 1D.

Wikipedia ha un riassunto abbastanza buono di tutto il processo . Per le sfere di qualsiasi massa, le nuove velocità possono essere calcolate usando le equazioni (dove v1 e v2 sono le velocità dopo la collisione, e u1, u2 sono precedenti):

Se le palle hanno la stessa massa, le velocità vengono semplicemente commutate. Ecco un po 'di codice che ho scritto che fa qualcosa di simile:

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

Per quanto riguarda l'efficienza, Ryan Fox ha ragione, dovresti considerare di dividere la regione in sezioni, quindi di effettuare il rilevamento delle collisioni all'interno di ciascuna sezione. Tieni presente che le palline possono scontrarsi con altre palline sui limiti di una sezione, quindi questo potrebbe rendere il tuo codice molto più complicato. L'efficienza probabilmente non importerà fino a quando non avrai diverse centinaia di palle. Per i punti bonus, è possibile eseguire ogni sezione su un nucleo diverso o suddividere l'elaborazione delle collisioni all'interno di ciascuna sezione.

Bene, anni fa ho realizzato il programma come te presentato qui.
C'è un problema nascosto (o molti, dipende dal punto di vista):

• Se la velocità della palla è troppo alta, puoi perdere la collisione.

Inoltre, quasi nel 100% dei casi le tue nuove velocità saranno sbagliate. Bene, non velocità , ma posizioni . Devi calcolare le nuove velocità esattamente nel posto giusto. Altrimenti basta spostare le palline su una piccola quantità di "errore", che è disponibile dal precedente passaggio discreto.

La soluzione è ovvia: devi dividere il timestep in modo tale che prima ti sposti nel posto giusto, poi ti scontri, poi cambi per il resto del tempo che hai.

È necessario utilizzare il partizionamento dello spazio per risolvere questo problema.

Leggi su Binary Space Partitioning e Quadtrees

Come chiarimento al suggerimento di Ryan Fox di dividere lo schermo in regioni e di verificare solo le collisioni all'interno delle regioni ...

ad es. dividere l'area di gioco in una griglia di quadrati (che dirà arbitrariamente di 1 unità di lunghezza per lato), e verificare la presenza di collisioni all'interno di ciascun quadrato della griglia.

Questa è assolutamente la soluzione corretta. L'unico problema con esso (come ha sottolineato un altro poster) è che le collisioni attraverso i confini sono un problema.

La soluzione a questo è quella di sovrapporre una seconda griglia ad un offset verticale e orizzontale di 0,5 unità rispetto alla prima.

Quindi, eventuali collisioni che si troverebbero oltre i confini della prima griglia (e quindi non rilevate) saranno all'interno dei quadrati della griglia nella seconda griglia. Finché tieni traccia delle collisioni che hai già gestito (poiché è probabile che si verifichino sovrapposizioni) non devi preoccuparti di gestire i casi limite. Tutte le collisioni saranno all'interno di una griglia su una delle griglie.

Un buon modo per ridurre il numero di controlli di collisione è dividere lo schermo in diverse sezioni. Quindi si confronta solo ogni palla con le palle nella stessa sezione.

Una cosa che vedo qui per ottimizzare.

Mentre concordo sul fatto che le palline colpiscono quando la distanza è la somma dei loro raggi, non si dovrebbe mai calcolare questa distanza! Piuttosto, calcola il quadrato e lavora in quel modo. Non c'è motivo per quella costosa operazione con radice quadrata.

Inoltre, una volta trovata una collisione, è necessario continuare a valutare le collisioni fino a quando non rimangono più. Il problema è che il primo potrebbe causare la risoluzione di altri che devono essere risolti prima di ottenere un'immagine precisa. Considera cosa succede se la palla colpisce una palla al limite? La seconda palla colpisce il bordo e rimbalza immediatamente nella prima palla. Se sbatti contro un mucchio di palline nell'angolo, potresti avere parecchie collisioni che devono essere risolte prima di poter ripetere il ciclo successivo.

Per quanto riguarda la O (n ^ 2), tutto ciò che puoi fare è minimizzare il costo del rifiuto di quelli che mancano:

1) Una palla che non si muove non può colpire nulla. Se sul pavimento è presente un numero ragionevole di palline, è possibile che si verifichino molti test. (Nota che devi ancora controllare se qualcosa ha colpito la palla ferma.)

2) Qualcosa che potrebbe valere la pena di fare: dividi lo schermo in un numero di zone ma le linee dovrebbero essere sfocate - le palline ai margini di una zona sono elencate in tutte le zone rilevanti (potrebbero essere 4). Vorrei utilizzare una griglia 4x4, memorizzare le zone come bit. Se un AND delle zone di due zone di sfere restituisce zero, fine del test.

3) Come ho già detto, non fare la radice quadrata.

Ho trovato una pagina eccellente con informazioni sul rilevamento delle collisioni e sulla risposta in 2D.

http://www.metanetsoftware.com/technique.html

Tentano di spiegare come viene fatto da un punto di vista accademico. Cominciano con il semplice rilevamento delle collisioni da oggetto a oggetto e passano alla risposta alla collisione e al modo di ridimensionarla.

Modifica: collegamento aggiornato

Hai due semplici modi per farlo. Jay ha spiegato il modo preciso di controllare dal centro della palla.

Il modo più semplice è utilizzare un rettangolo di selezione, impostare la dimensione del riquadro in modo che sia l'80% della dimensione della palla e simulerai abbastanza bene la collisione.

Aggiungi un metodo alla tua classe di palla:

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

Quindi, nel tuo ciclo:

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

Vedo che è accennato qua e là, ma potresti anche fare prima un calcolo più veloce, ad esempio, confrontare i riquadri di delimitazione per la sovrapposizione e ALLORA fare una sovrapposizione basata sul raggio se il primo test viene superato.

La matematica addizione / differenza è molto più veloce per un riquadro di delimitazione rispetto a tutti i trigoni per il raggio e, la maggior parte delle volte, il test del riquadro di delimitazione eliminerà la possibilità di una collisione. Ma se poi riesegui nuovamente il test con Trig, otterrai i risultati precisi che stai cercando.

Sì, sono due test, ma nel complesso sarà più veloce.

Questa KineticModelè un'implementazione dell'approccio citato in Java.

Ho implementato questo codice in JavaScript usando l'elemento HTML Canvas e ha prodotto meravigliose simulazioni a 60 frame al secondo. Ho iniziato la simulazione con una raccolta di una dozzina di palline a posizioni e velocità casuali. Ho scoperto che a velocità più elevate, una collisione occhiata tra una pallina e una molto più grande ha fatto apparire la pallina attaccarsi al bordo della sfera più grande, e si è spostata di circa 90 gradi attorno alla sfera più grande prima di separarsi. (Mi chiedo se qualcun altro abbia osservato questo comportamento.)

Alcune registrazioni dei calcoli hanno mostrato che la distanza minima di traduzione in questi casi non era abbastanza grande da impedire alle stesse sfere di scontrarsi nella fase successiva. Ho fatto alcuni esperimenti e ho scoperto che potevo risolvere questo problema aumentando l'MTD in base alle velocità relative:

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

Ho verificato che prima e dopo questa correzione, l'energia cinetica totale veniva conservata per ogni collisione. Il valore 0,5 in mtd_factor era approssimativamente il valore minimo trovato per causare sempre la separazione delle sfere dopo una collisione.

Sebbene questa correzione introduca una piccola quantità di errore nell'esatta fisica del sistema, il compromesso è che ora le sfere molto veloci possono essere simulate in un browser senza ridurre le dimensioni del passo temporale.