Perché la ricottura quantistica non può essere descritta da un modello di gate?

Questa è una domanda che mi ha ispirato a porre sulla base di questa domanda , che rileva che la ricottura quantistica è un modello di calcolo completamente diverso rispetto al solito modello di circuito. L'ho già sentito prima, ed è la mia comprensione che il modello di gate non si applica alla ricottura quantistica, ma non ho mai capito bene perché sia ​​così o come analizzare i calcoli che un ricottista può fare. Come ho capito da diversi colloqui (alcuni degli stessi D-wave!), Il fatto che gli annealer siano limitati a uno specifico gioco Hamiltoniano in esso.

Un ricottura quantistica, come una macchina D-Wave, è una rappresentazione fisica del modello Ising e come tale ha un 'problema' hamiltoniano della forma

$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

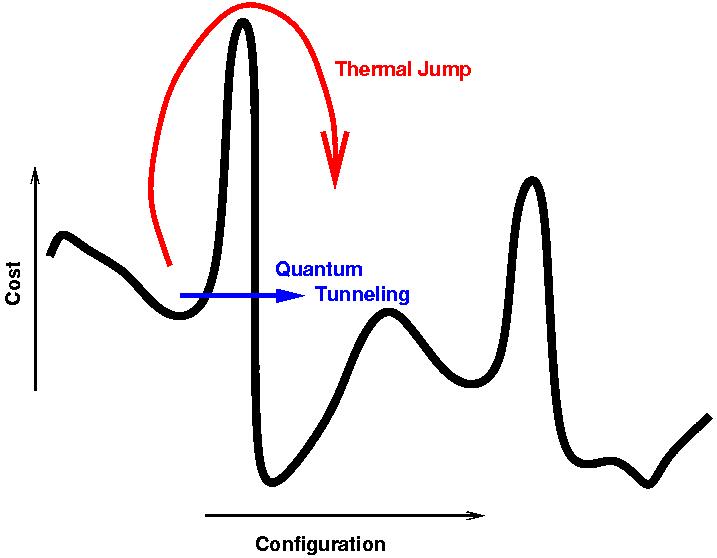
Poiché si tratta di una ricottura, il processo viene eseguito abbastanza lentamente da rimanere vicino allo stato fondamentale del sistema mentre l'Hamiltoniano è variato a quello del problema, usando il tunneling per rimanere vicino allo stato fondamentale come descritto nella risposta di Nat .

Ora, perché questo non può essere usato per descrivere un QC modello gate? Quanto sopra è un problema di ottimizzazione binaria non vincolata quadratica (QUBO) , che è NP-difficile ... In effetti, ecco un articolo che mappa un numero di problemi NP al modello Ising . Qualsiasi problema in NP può essere associato a qualsiasi problema NP-difficile nel tempo polinomiale e la fattorizzazione a numeri interi è effettivamente un problema NP.

$0.2\%$

Ciò che (in linea di principio) fa è avvicinarsi molto al risultato esatto, molto rapidamente, ma ciò non aiuta per nulla in cui è richiesto il risultato esatto in quanto passare da "quasi corretto" a "corretto" è ancora estremamente difficile ( vale a dire presumibilmente ancora NP in generale, quando il problema originale è in NP) problema in questo caso, poiché i parametri che sono / danno una soluzione "quasi corretta" non saranno necessariamente distribuiti ovunque vicino ai parametri che sono / danno soluzione corretta.

Modifica per chiarimento: ciò significa che un dispositivo di ricottura quantistica (QA) richiede ancora tempo esponenziale (anche se potenzialmente un tempo esponenziale più veloce) per risolvere problemi NP come la fattorizzazione a numeri interi, in cui un controllo di qualità universale dà una velocità esponenziale e può risolvere lo stesso problema in poli tempo. Questo è ciò che implica che un QA non può simulare un QC universale in poly time (altrimenti potrebbe risolvere problemi in poly time che non può). Come sottolineato nei commenti, ciò non equivale a dire che un QA non può fornire la stessa velocità in altri problemi, come la ricerca nel database.

La ricottura è più una tattica analogica.

L'essenza è che hai qualche strana funzione che vuoi ottimizzare. Quindi, ci rimbalzi intorno. Inizialmente, la " temperatura " è molto alta, in modo che il punto selezionato possa rimbalzare molto. Quindi quando l'algoritmo "si raffredda ", la temperatura scende e il rimbalzo diventa meno aggressivo.

Alla fine, si stabilisce in un optima locale che, idealmente, è favorevolmente come il optima globale.

Ecco un'animazione per la ricottura simulata (non quantistica):

Ma è praticamente lo stesso concetto per la ricottura quantistica :

Al contrario, la logica di gate è molto più digitale che analogica. Si occupa di qubit e operazioni logiche piuttosto che semplicemente di trovare un risultato dopo un caotico rimbalzo.