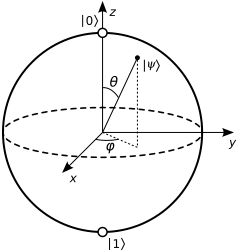
Come pensare al cancello Z in una sfera Bloch?

10

Sono confuso su come capire la porta $Z$ in una sfera Bloch.

Considerando la matrice è comprensibile che e . $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

Qui viene spiegato che la porta $Z$ è una rotazione $\pi$ attorno all'asse $Z$ Quindi, come dovrei capire $Z|1\rangle = -|1\rangle$ ? Dal $|1\rangle$ è il polo sud, sento che è naturale pensare che $\pi$ rotazione attorno $Z$ all'asse non fa nulla.

quantum-gate bloch-sphere

— Bick
fonte

7

Il modo di pensare alla sfera di Bloch è in termini di matrice di densità per lo stato. agisce su o non fa nulla, come è vero per qualsiasi matrice di densità diagonale. Per vedere l'effetto della rotazione, devi guardare come una matrice di densità non diagonale viene modificata da , come . $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

— DaftWullie
fonte

7

e vengono assegnati allo stesso punto sulla sfera Bloch perché sono ugualifino a fase globale. Algebricamente: dove significa "uguale fino a fase globale". Significa che c'è un tale che . $|1\rangle$ $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

La cosa che ti confonde è che, nonostante il fatto che e , ciò non vale per combinazioni lineari dei due. Ad esempio, Anche se $|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ . $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

— Craig Gidney
fonte

2

Come da Wikipedia , possiamo scrivere qualsiasi stato puro come

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Dove e sono gli angoli sulla sfera Bloch: $\theta$ $\phi$

Quasi ogni punto sulla superficie (cioè lo stato puro) ha una rappresentazione unica in termini di angoli, ad eccezione dei poli. Proprio come sulla Terra, il Polo Sud non ha una longitudine ben definita (qualsiasi longitudine funziona allo stesso modo), per il stato alcuna fase significa la stessa cosa. Il “latitudine” è qui , cerchiamo di tappo che nella equazione: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Se hai familiarità con l'identità di Eulero, probabilmente riconoscerai come una rotazione nel piano complesso. In particolare, poiché è una rotazione per , otteniamo il famoso , arrivando infine a . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

— Norrius
fonte

1

Questo è sbagliato. Scrivere

è fuorviante: questi sono stati equivalenti in quanto differiscono solo per una fase globale, ma questo non significa che i vettori di stato sono uguali. Ottieni questo risultato perché stai assumendo che ci sia una biiezione tra vettori di stato e punti sulla sfera di Bloch, il che non è il caso. La biiezione si trova tra i punti sulla sfera di Bloch e gli stati descritti come matrici di densità

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

— glS

@glS Grazie, l'

che ne consegue sembrava sospetto. Ha senso migliorare quella risposta dal tuo punto di vista o è irrimediabilmente sbagliato?

1 = - 1

$1=-1$

— Norrius,

questa è la tua chiamata =). Penso che la risposta corretta sia quella data da DaftWullie (credo che il richiedente abbia avuto un equivoco simile a quello nella tua risposta). Non vedo molto da dire su questa domanda

— glS