In cosa consiste il teorema di Bayes?

Quali sono le idee principali, cioè i concetti relativi al teorema di Bayes ? Non sto chiedendo alcuna derivazione di complessa notazione matematica.

Il teorema di Bayes è un risultato relativamente semplice, ma fondamentale della teoria della probabilità che consente il calcolo di alcune probabilità condizionali. Le probabilità condizionali sono solo quelle probabilità che riflettono l'influenza di un evento sulla probabilità di un altro.

In poche parole, nella sua forma più famosa, afferma che la probabilità di un'ipotesi dati nuovi dati ( P (H | D) ; chiamata probabilità posteriore) è uguale alla seguente equazione: la probabilità dei dati osservati data l'ipotesi ( P (D | H) ; chiamata probabilità condizionale), moltiplicata per la probabilità che la teoria sia vera prima di nuove prove ( P (H) ; chiamata probabilità precedente di H), divisa per la probabilità di vedere tali dati, periodo ( P (D ); chiamata probabilità marginale di D).

Formalmente, l'equazione si presenta così:

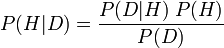
Il significato del teorema di Bayes è in gran parte dovuto al suo uso corretto essendo un punto di contesa tra scuole di pensiero sulla probabilità. A un bayesiano soggettivo (che interpreta la probabilità come gradi di credenza soggettivi) il teorema di Bayes fornisce la pietra angolare per i test teorici, la selezione della teoria e altre pratiche, inserendo i loro giudizi di probabilità soggettivi nell'equazione e correndo con esso. Per un frequentatore (che interpreta la probabilità come frequenze relative limitanti ), questo uso del teorema di Bayes è un abuso, e si sforzano invece di usare priori significativi (non soggettivi) (così come i bayesiani obiettivi sotto un'altra interpretazione della probabilità).

Mi dispiace, ma qui sembra esserci un po 'di confusione: il teorema di Bayes non è in discussione per il dibattito senza fine Bayesiano- Frequentista . È un teorema coerente con entrambe le scuole di pensiero (dato che è coerente con gli assiomi di probabilità di Kolmogorov).

Naturalmente, il teorema di Bayes è il nucleo delle statistiche bayesiane, ma il teorema stesso è universale. Lo scontro tra frequentisti e bayesiani riguarda principalmente il modo in cui le distribuzioni precedenti possono essere definite o meno.

Quindi, se la domanda riguarda il teorema di Bayes (e non le statistiche bayesiane):

Il teorema di Bayes definisce come si possono calcolare specifiche probabilità condizionali. Immagina per esempio di sapere: la probabilità che qualcuno abbia il sintomo A, dato che ha la malattia X p (A | X); la probabilità che qualcuno in generale abbia la malattia X p (X); la probabilità che qualcuno in generale abbia il sintomo A p (A). con queste 3 informazioni puoi calcolare la probabilità che qualcuno abbia la malattia X, dato che ha il simbolo A p (X | A).

Il teorema di Bayes è un modo per ruotare una probabilità condizionale su un'altra probabilità condizionale P ( B | A ) .$P(A|B)$$P(B|A)$

Un ostacolo per alcuni è il significato di . Questo è un modo per ridurre lo spazio di possibili eventi considerando solo quegli eventi in cui A si verifica (o è vero). Quindi, ad esempio, la probabilità che un dado lanciato, giusto, atterra mostrando sei, P ( dadi atterra sei ) , è 1/6, tuttavia la probabilità che un dado atterra sei dato che ha ottenuto un numero pari, P ( dadi atterra sei | il dado atterra anche ) , è 1/3.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

Puoi derivare te stesso il teorema di Bayes come segue. Inizia con la definizione del rapporto di una probabilità condizionale:

$P(B|A) = \frac{P(AB)}{P(A)}$

dove è la probabilità congiunta di A e B e P ( A ) è la probabilità marginale di A .$P(AB)$$A$$B$$P(A)$$A$

Attualmente la formula non fa riferimento a , quindi scriviamo anche la definizione di questo:$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

e hey presto:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

Per quanto riguarda lo scopo di ruotare una probabilità condizionale in questo modo, considera l'esempio comune di provare a inferire la probabilità che qualcuno abbia una malattia dato che hanno un sintomo, cioè sappiamo che hanno un sintomo - possiamo semplicemente vederlo - ma non possiamo essere certi che abbiano una malattia e debbano dedurla. Inizierò con la formula e tornerò indietro.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

Quindi, per risolverlo, è necessario conoscere la probabilità precedente del sintomo, la probabilità precedente della malattia (cioè, quanto comuni o rari sono il sintomo e la malattia) e anche la probabilità che qualcuno abbia un sintomo dato che sappiamo che qualcuno ha una malattia (ad es. tramite costosi test di laboratorio).

Può diventare molto più complicato di così, ad esempio se hai più malattie e sintomi, ma l'idea è la stessa. Ancora più in generale, il teorema di Bayes appare spesso se si ha una teoria delle probabilità delle relazioni tra cause (ad es. Malattie) ed effetti (ad es. Sintomi) e si deve ragionare all'indietro (ad es. Si vedono alcuni sintomi da cui si desidera inferire la malattia di base).

Esistono due principali scuole di pensiero: Statistica: frequentista e bayesiana .

Il teorema di Bayes ha a che fare con quest'ultimo e può essere visto come un modo per capire come la probabilità che una teoria sia vera è influenzata da una nuova prova. Questo è noto come probabilità condizionale. Potresti voler guardare questo per avere una conoscenza della matematica.

Lascia che ti dia una visione molto molto intuitiva. Supponi di lanciare una moneta 10 volte e di ottenere 8 teste e 2 code. La domanda che ti verrà in mente è se questa moneta è distorta o meno verso le teste.

Ora, se segui le definizioni convenzionali o l'approccio frequentista della probabilità, potresti dire che la moneta è imparziale e questo è un evento eccezionale. Quindi concluderesti che anche la possibilità di ottenere un lancio successivo è del 50%.

Ma supponi di essere un bayesiano. Penseresti davvero che, dato che hai un numero eccezionalmente alto di teste, la moneta ha una propensione verso la testa. Esistono metodi per calcolare questo possibile pregiudizio. Li calcoleresti e poi la prossima volta che lanci la moneta, chiameresti sicuramente una testa.

Quindi, la probabilità bayesiana riguarda la convinzione che sviluppi sulla base dei dati che osservi. Spero fosse abbastanza semplice.

Il teorema di Bayes mette in relazione due idee: probabilità e probabilità. La probabilità dice: dato questo modello, questi sono i risultati. Quindi: dato una moneta giusta, avrò la testa il 50% delle volte. Likelihood dice: visti questi risultati, questo è ciò che possiamo dire sul modello. Quindi: se lanci una moneta 100 volte e ottieni 88 teste (per raccogliere un esempio precedente e renderlo più estremo), allora la probabilità che il modello di moneta giusta sia corretta non è così alta.

Uno degli esempi standard usati per illustrare il teorema di Bayes è l'idea di testare una malattia: se fai un test con un'accuratezza del 95% per una malattia che 1 su 10000 della popolazione ha, e sei positivo, quali sono le possibilità che hai la malattia?

La risposta ingenua è del 95%, ma questo ignora il problema che il 5% dei test su 9999 su 10000 persone darà un falso positivo. Quindi le tue probabilità di avere la malattia sono molto inferiori al 95%.

Il mio uso della vaga frase "quali sono le possibilità" è deliberato. Per usare il linguaggio probabilità / probabilità: la probabilità che il test sia accurato è del 95%, ma ciò che vuoi sapere è la probabilità che tu abbia la malattia.

Un po 'fuori tema: l'altro classico esempio che il teorema di Bayes è usato per risolvere in tutti i libri di testo è il problema di Monty Hall: sei su un quiz. C'è un premio dietro una delle tre porte. Scegli la prima porta. L'host apre la terza porta per non rivelare alcun premio. Dovresti passare alla seconda porta, data la possibilità?

Mi piace la riformulazione della domanda (per gentile concessione del riferimento di seguito): sei su un quiz. C'è un premio dietro una delle milioni di porte. Scegli la prima porta. L'host apre tutte le altre porte tranne la porta 104632 per non rivelare alcun premio. Dovresti cambiare alla porta 104632?

Il mio libro preferito che discute del teorema di Bayes, molto dalla prospettiva bayesiana, è "Teoria dell'informazione, inferenza e algoritmi di apprendimento", di David JC MacKay. È un libro della Cambridge University Press, ISBN-13: 9780521642989. La mia risposta è (spero) una distillazione del tipo di discussioni fatte nel libro. (Si applicano le solite regole: non ho affiliazioni con l'autore, mi piace solo il libro).

Il teorema di Bayes nella sua forma più ovvia è semplicemente una riaffermazione di due cose:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

Quindi usando la simmetria:

$P(D|I) \neq 0$$P(D|I)$

So this is it? How can something so simple be so awesome? As with most things "its the journey that's more important than the destination". Bayes theorem rocks because of the arguments that lead to it.

Ciò che manca da ciò è che la regola del prodotto e la regola della somma $P(H|I)=1-P(\overline{H}|I)$, può essere derivato usando la logica deduttiva basata su assiomi di ragionamento coerente.

Ora la "regola" nella logica deduttiva è che se hai una relazione "A implica B" allora hai anche "Non B implica Non A". Quindi abbiamo "un ragionamento coerente implica il teorema di Bayes". Ciò significa che "il teorema di Not Bayes implica un ragionamento non coerente". vale a dire se il risultato non equivale a un risultato bayesiano per alcuni precedenti e verosimili, allora stai ragionando in modo incoerente.

Questo risultato si chiama teorema di Cox ed è stato dimostrato in "Algebra della probabile inferenza" negli anni '40. Una derivazione più recente è data nella teoria della proabilità: la logica della scienza.

I really like Kevin Murphy's intro the to Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

The quote here is from an economist article:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

L'essenza dell'approccio bayesiano è fornire una regola matematica che spieghi come dovresti cambiare le tue convinzioni esistenti alla luce di nuove prove. In altre parole, consente agli scienziati di combinare nuovi dati con le loro conoscenze o competenze esistenti. L'esempio canonico è immaginare che un neonato precoce osservi il suo primo tramonto e si chieda se il sole sorgerà o meno. Assegna le stesse precedenti probabilità a entrambi i possibili risultati e lo rappresenta mettendo un marmo bianco e uno nero in una borsa. Il giorno seguente, quando sorge il sole, il bambino mette un altro marmo bianco nella borsa. La probabilità che un marmo strappato casualmente dalla borsa sia bianco (cioè il grado di fiducia del bambino nelle future albe) è quindi passata da metà a due terzi. Dopo l'alba del giorno successivo, il bambino aggiunge un altro marmo bianco e la probabilità (e quindi il grado di credenza) va dai due terzi ai tre quarti. E così via. A poco a poco, la convinzione iniziale che il sole abbia la stessa probabilità di non sorgere ogni mattina viene modificata per diventare quasi una certezza che il sole sorgerà sempre.