Cosa indica una forma a cuneo del diagramma PCA?

Nel loro documento sulla autoencoders per la classificazione di testo Hinton e Salakhutdinov dimostrato la trama prodotta da 2-dimensionale LSA (che è strettamente legata alla PCA): .

Applicando la PCA a dati dimensionali leggermente diversi e assolutamente diversi ho ottenuto una trama dall'aspetto simile: (tranne in questo caso, volevo davvero sapere se c'è una struttura interna).

Se inseriamo dati casuali nel PCA otteniamo un blob a forma di disco, quindi questa forma a cuneo non è casuale. Significa qualcosa da solo?

Supponendo che le variabili siano positive o non negative, i bordi del bordo sono solo punti oltre i quali i dati diverrebbero rispettivamente 0 o negativi. Poiché tali dati della vita reale tendono ad essere distorti, vediamo una maggiore densità di punti nella parte bassa della loro distribuzione e quindi una maggiore densità nel "punto" del cuneo.

Più in generale, PCA è semplicemente una rotazione dei dati e i vincoli su tali dati saranno generalmente visibili nei componenti principali nello stesso modo mostrato nella domanda.

Ecco un esempio che utilizza diverse variabili log-normalmente distribuite:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

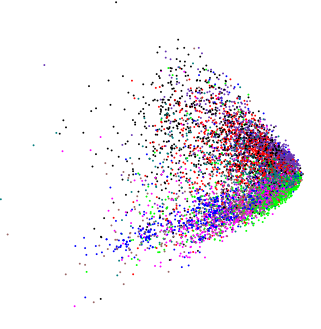
A seconda della rotazione implicita dai primi due PC, potresti vedere il cuneo o potresti vedere una versione leggermente diversa, mostrala qui in 3d usando ( ordirgl()al posto di plot())

Qui, in 3d, vediamo più punte sporgenti dalla massa centrale.

$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

E per variabili casuali positive uniformi vediamo un cubo

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Nota che qui, per l'illustrazione, mostro l'uniforme usando solo 3 variabili casuali, quindi i punti descrivono un cubo in 3d. Con dimensioni maggiori / più variabili non possiamo rappresentare l'ipercubo 5d perfettamente in 3d e quindi la distinta forma del "cubo" viene distorta in qualche modo. Problemi simili influiscono sugli altri esempi mostrati, ma è comunque facile vedere i vincoli in quegli esempi.

Per i tuoi dati, una trasformazione del log delle variabili prima del PCA tirerebbe le code e allungherebbe i dati raggruppati, proprio come potresti usare una tale trasformazione in una regressione lineare.

Altre forme possono apparire nei grafici PCA; una di queste forme è un manufatto della rappresentazione metrica conservata nel PCA ed è conosciuta come il ferro di cavallo . Per i dati con un gradiente lungo o dominante (i campioni disposti lungo una singola dimensione con variabili che aumentano da 0 a un massimo e poi si riducono di nuovo a 0 lungo porzioni di dati sono ben noti per generare tali artefatti.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

che produce un ferro di cavallo estremo, dove i punti alle estremità degli assi si piegano di nuovo nel mezzo.