Quale distribuzione viene più comunemente utilizzata per modellare i tempi di risposta del server?

Ho un'applicazione basata su servlet in cui misuro il tempo impiegato per completare ogni richiesta a quel servlet. Calcolo già statistiche semplici come media e massima; Vorrei comunque produrre alcune analisi più sofisticate, e per farlo credo di dover modellare correttamente questi tempi di risposta.

Sicuramente, dico, i tempi di risposta seguono una distribuzione ben nota e ci sono buone ragioni per ritenere che la distribuzione sia il modello giusto. Tuttavia, non so quale dovrebbe essere questa distribuzione.

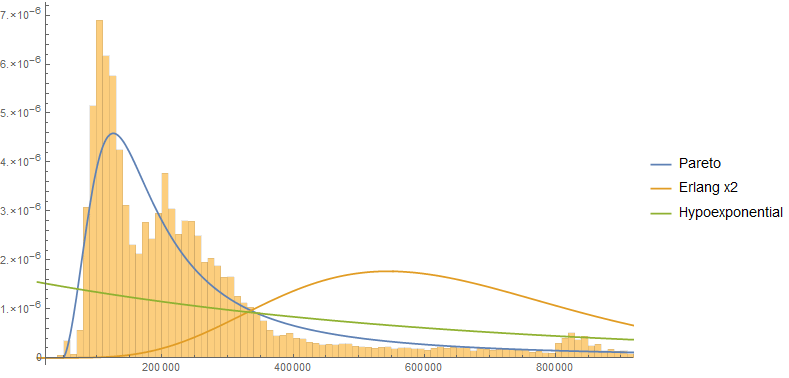
Log-normal e Gamma vengono in mente e puoi creare uno dei due dati di tempo di risposta reali. Qualcuno ha una visione su quale distribuzione dovrebbero seguire i tempi di risposta?

La distribuzione Log-Normal è quella che trovo migliore nel descrivere le latenze dei tempi di risposta del server in tutta la base di utenti per un periodo di tempo.

È possibile visualizzare alcuni esempi nel sito lognormal.com dal nome appropriato, il cui compito è misurare la distribuzione della latenza del sito nel tempo e altro ancora. Non ho alcuna affiliazione con il sito se non per essere un utente felice. Ecco come appare la distribuzione; tempo di risposta (ad es. caricamento della pagina Web) rispetto al numero di risposte:

Si noti che in questo grafico, la scala del tempo di caricamento (asse X) è lineare. Se si sposta l'asse x su una scala logaritmica, la forma della distribuzione sembrerebbe più normale (a forma di campana) sul lato destro del picco.

La mia ricerca mostra che il modello migliore è determinato da alcune cose: 1) Ti preoccupi del corpo, della coda o di entrambi? Se non "entrambi", la modellazione di un set di dati filtrato può essere più utile. 2) Ne vuoi uno molto semplice o molto preciso? cioè quanti parametri?

Se la risposta a 1 era "entrambi" e 2 era "semplice", Pareto sembra funzionare meglio. Altrimenti, se 1 fosse "corpo" e 2 fosse "semplice", scegli un modello di filtro erlang. Se 1 era "entrambi" e 2 era "accurato", probabilmente vorrai un modello di miscela gaussiana sui tuoi dati nel dominio dei log - in effetti un adattamento lognormale.

Recentemente ho fatto ricerche su questo argomento e non ho trovato l'argomento da trattare abbastanza bene su Internet pubblico, quindi ho appena scritto un post sul blog che illustra in dettaglio la mia ricerca su questo argomento.