Come si trasforma un cubo in una sfera?

Sto cercando di creare una sfera quadrupla basata su un articolo , che mostra risultati come questo:

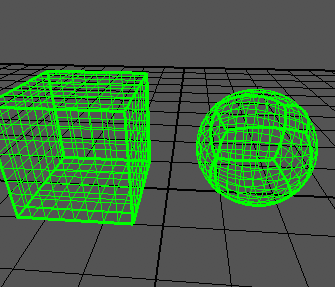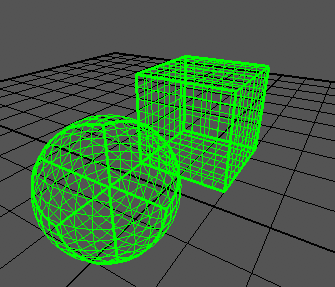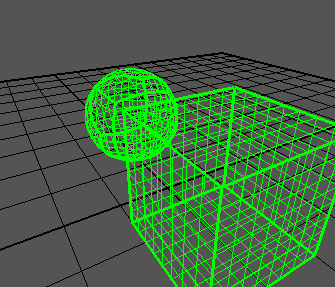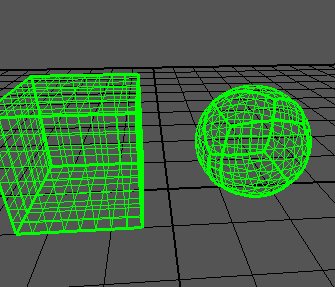
Posso generare correttamente un cubo:

Ma quando converto tutti i punti secondo questa formula (dalla pagina collegata sopra):

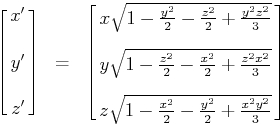
    x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
    y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
    z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

La mia sfera si presenta così:

Come puoi vedere, i bordi del cubo sporgono ancora troppo. Il cubo va da -1a +1tutti gli assi, come dice l'articolo.

Qualche idea di cosa non va?

Hai sbagliato a scrivere la formula.

x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Modifichi l'originale xe lo sovrascrivi. Quindi si modifica ynon in base all'originale xma a quello modificato x. Quindi si modifica in zbase alla versione modificata di entrambi .

Conserva gli originali e calcola questo:

float dx = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
float dy = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
float dz = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Usa dx, dy e dz da allora in poi.