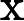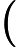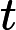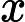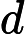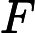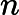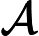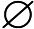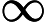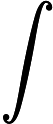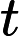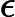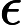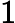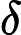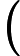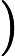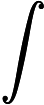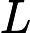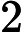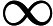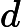Credo che il tuo professore di econometria stesse pensando a qualcosa come segue.
Considera la funzione con domiain definita da[ 0 , 1 ]





F(x)=1
Questa è una funzione discontinua, ma un CDF completamente valido per una certa distribuzione di probabilità su . Si noti che, utilizzando questa distribuzione




Non esiste alcuna funzione che funge da PDF per questa distribuzione, anche se esiste un CDF.
È abbastanza facile verificare che ciò sia vero in questo semplice esempio se hai già visto questo genere di cose. Supponiamo che esista un pdf , mostreremo che deve avere una proprietà impossibile, e quindi non può esistere.
Per definizione di un PDF, dobbiamo avere
per tutti . Una funzione che si integra con una funzione lineare deve essere costante (tecnicamente costante quasi ovunque), quindi concludiamo che





Allo stesso modo, ma integrando a partire da uno, spostandoci verso zero e finendo con , arriviamo alla stessa conclusione



Quindi abbiamo determinato ovunque tranne . Ma non importa cosa sia , non può avere la proprietà di integrazione desiderata. Da




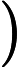




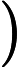
avremmo bisogno
per ogni intervallo contenente . Ma in effetti il valore di qualsiasi integrale non viene influenzato modificando il valore di una funzione in un singolo punto, quindi

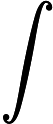



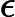



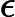


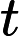


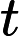

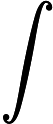



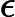



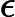



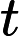



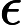
Quindi non c'è via d'uscita, una funzione come non può esistere.
Puoi recuperare lo spirito di un PDF, ma devi usare oggetti matematici più sofisticati, una misura o una distribuzione .
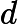
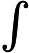 R
R